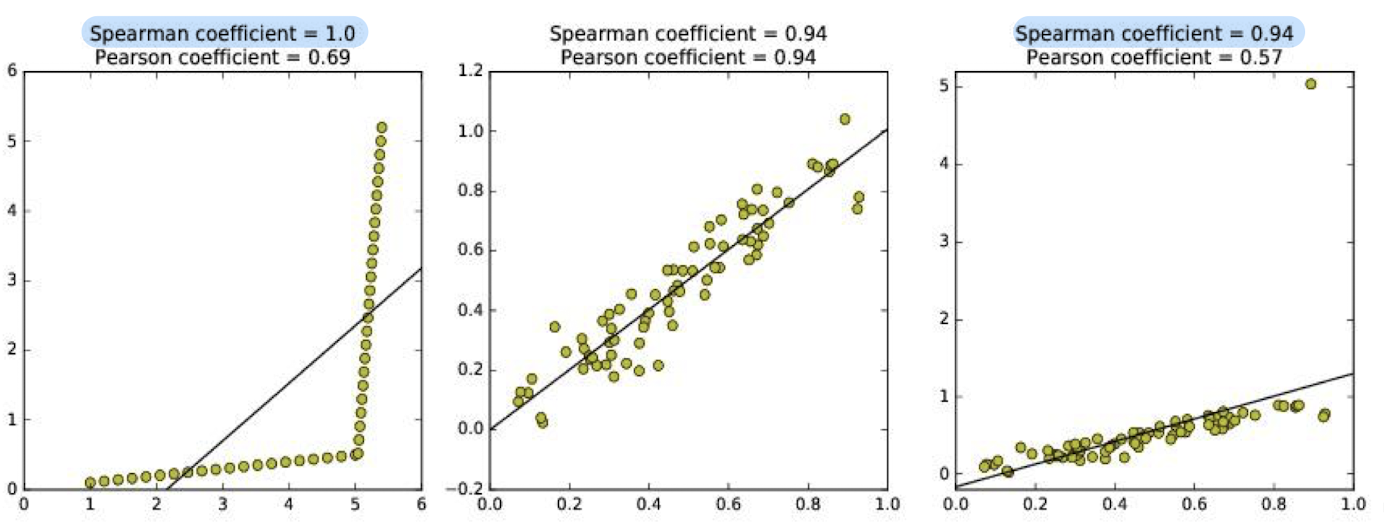
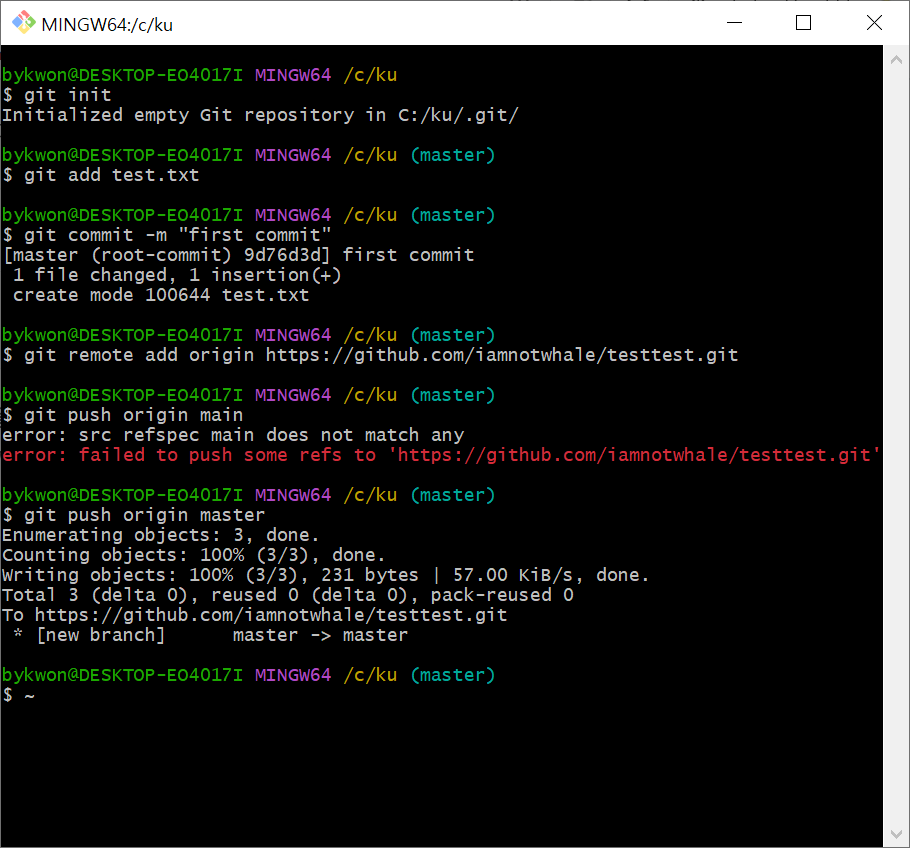
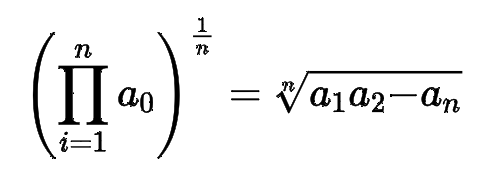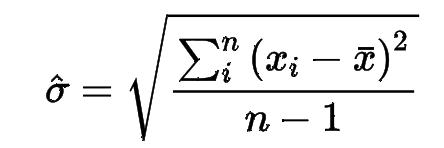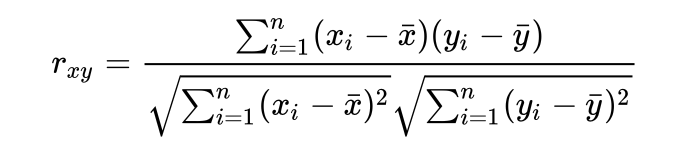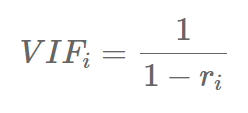Typical Data Science Pipeline
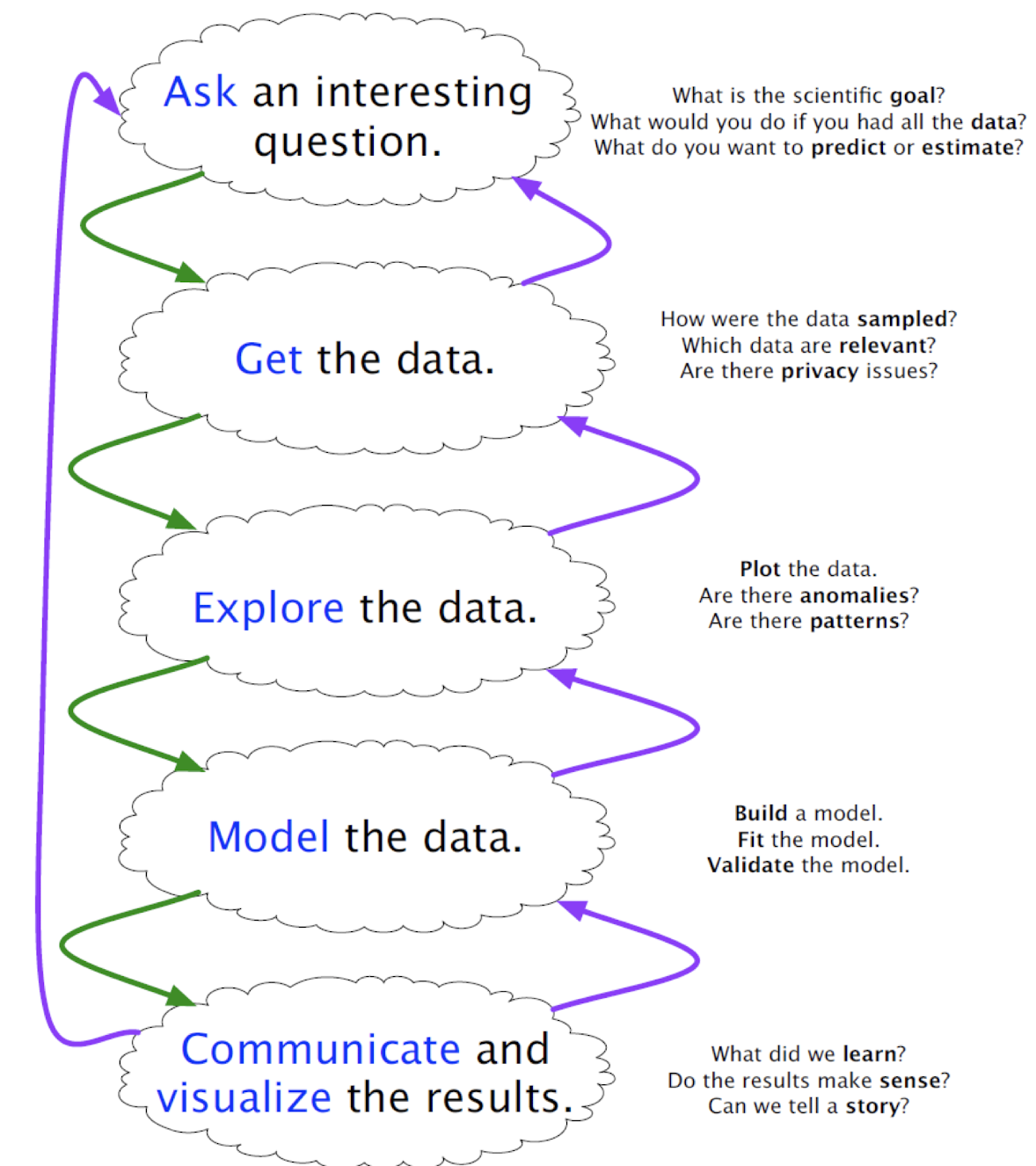
Data Munging / Data wrangling
- 데이터를 얻고 분석을 위해 준비/정리하는 것
데이터과학에 사용하는 언어
- Python: 라이브러리, 피쳐 등 포함 - regular expressions
* regular expression 예
- [hc]at : hat or cat
- .at : .자리에 아무거나 들어갈 수 있음
- ab*c : b가 0개 이상 있어야 함
- ab+c : b가 1개 이상 있어야 함
- R: 통계학자들이 주로 사용
- Matlab: 행렬
- Java/C++: 빅데이터 시스템을 위한 언어
- Excel: bread and butter toool
노트북 환경
- reproducible, tweakable, documented
- 데이터 파이프라인을 유지하기 쉽다.
데이터 수집
- Files (CSV, XML, JSON)
- Databases (SQL server)
- API: Application Programming Interface
- Web Scraping (HTML)
데이터 형식
1. CSV (Comma-Separated Values)
2. XML (eXtensible Markup Language)
<student>
<name> 000 </name>
<age> 19 </age>
</student>
이런 식으로 <>, </> 로 구분 가능
3. JSON (JavaScript Object Notation)
{
"a": {
"name": 000,
"age": 19
}
... 이런 식으로, {}와 따옴표 등으로 구분
CSV 파일에서 데이터 불러오기 - pandas 이용
import pandas
student_data = pandas.read_csv("student_table.csv")
Relational DB에서 데이터 불러오기
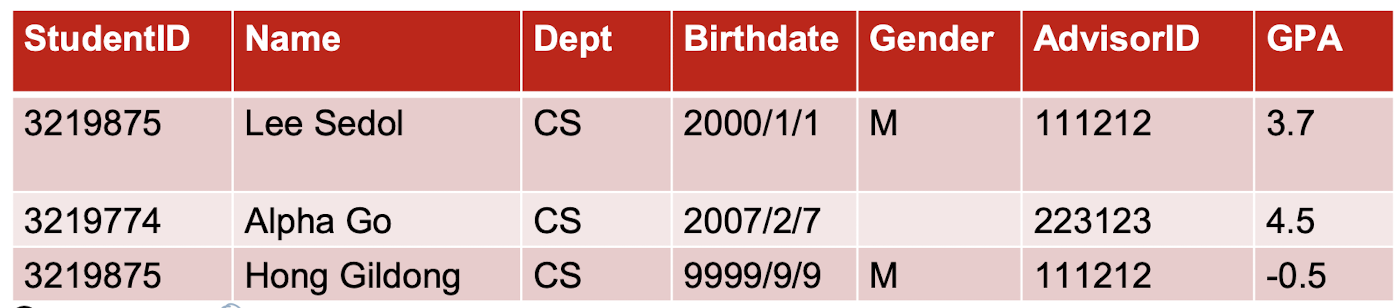
import pandas
student_data = pandas.read_sql_query(sql_string, db_uri)SELECT * FROM student_table --전체 불러오기
SELECT studentid, name FROM student_table WHERE gpa > 3.5
--테이블에서 gpa>3.5인 학생들의 id와 이름 불러오기
SELECT S.name, A.name
FROM student_table S, advisor_table A
WHERE S.advisorid = A.id --학생의 지도교수 아이디가 지도교수 명단 아이디와 동일한 경우에 이름 쌍 출력
SELECT S.advisorid, avg(S.gpa)
FROM student_table S
GROUP BY S.advisorid --지도교수가 같은 학생들의 지도교수 아이디와 학생들 성적 평균 출력
SELECT S.advisorid, avg(S.gpa)
FROM student_table S
WHERE S.birthdate >= 2000/1/1 AND S.birthdate < 2010/1/1
GROUP BY S.advisorid
API를 이용하여 데이터 얻기
- REST (Representational State Transfer) API
import json
import requests
url = 'https://...format=json'
data = requests.get(url).text
parsed_data = json.loads(data)
Web Scraping
<html>
<head>
<title> ... </title>
</head>
<body>
<h1> hello world! </h1>
<p> COSE471 data science </p>
</body>
</html>
데이터의 원천
1. Proprietary Data Sources
- 기업이 수집하는 내부 데이터
- API로 제한적으로 공개할 수 있음
- 외부로 데이터 전체를 공개하기 어려운 이유: 비즈니스적 이유(경쟁사를 도와줄 수 있음), 프라이버시 이슈
- 예시: 2006년 AOL search log release
2. Government Data Sources
- 시, 국가 등에서 공개하는 오픈 데이터
- Freedom of Information Act: 데이터를 공개해달라고 요청할 수 있음
- 데이터가 공개될 때 프라이버시를 지켜야 함
3. Academic Data Sets
- 논문 등에서 발표하는 자료
4. Web Search/Scraping
- Scraping: 웹페이지에서 데이터나 텍스트를 추출하는 것
- 이미 API가 존재하는지, 누군가 이미 scraper를 작성해두었는지 확인하고 해야 함
5. Available Data Sources
- Bulk Downloads: 위키피디아, IMDB, Million Song Database
- API access: 뉴욕타임스, 트위터 등
6. Sensor Data Logging
- 이미지, 비디오 데이터: Flicker 이미지를 이용하여 날씨를 관측
- 휴대폰의 accelerometer를 이용하여 지진 관측
- 택시 GPS를 이용하여 교통 흐름 관측
- logging system 구축: 저장소가 저렴함
7. Crowdsourcing
- 위키피디아, Freebase, IMDB 등 여러 저자가 참여한 데이터
- Amazon Turk, CrowdFlower 등의 플랫폼에 돈을 지불하면 다수의 사람이 데이터를 모아올 수 있음
8. Sweat Equity
- 역사 자료 등은 종이, 피디에프 등의 형식으로 저장되어있어 변환이 필요함
Cleaning Data: Garbage In, Garbage Out
- 데이터 정리 중에 나타날 수 있는 문제
* artifact와 오류를 구별
* Data compatibility, unification
* 결측치 처리
* 미관측값 (0) 추정
* 이상치 탐지
Errors vs. Artifacts
- error: 데이터를 수집하는 과정에서 근본적으로 잃어버린 정보
- artifact: 데이터 처리 과정 중에 나타나는 시스템적인 문제
- sniff test: product를 가까이에서 조사하여 잘못되었다는 낌새를 알아차리는 방법
연도별 과학자의 첫 논문 발표자 수 관련 데이터
- PubMed를 이용하여 가장 자주 인용되는 과학자 100,000명의 첫 논문 발표 연도를 조사
- 예상 분포: 1960년에 몰려있고, 2023년에 가까워지면 0에 수렴하며, 그 중간은 일정하게 유지되는 그래프
(이유: 1960년부터 데이터를 수집했으므로 그 이전 논문들도 1960년으로 반영될 수 있으며, 최근에 가까워질수록 커리어가 적은 사람이 많아서 순위에 들지 못할 가능성이 높음)
- 실제 분포 (왼쪽)
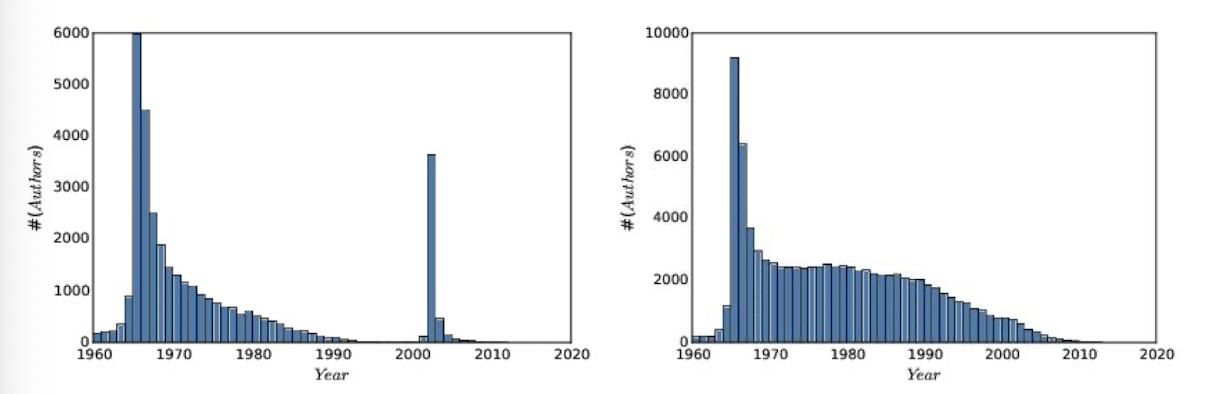
1965년 이전 데이터는 수작업으로 하여 누락되었을 가능성 있음
2000년 이후 저자 이름 기록 방식이 변화로, 다른 저자지만 같은 저자로 인식할 수 있어 오류 발생
Data Compatibility
1. Unit Conversion
- 1999년 나사의 Mars Climate Orbiter가 사라짐
- 이유는 단위 차이 때문
- Z-score를 이용하면 단위가 사라지므로 유용
2. Number / Character Representation
- 1996년 Ariane 5 rocket 폭발: 64-bit float을 16-bit integer로 전환했기 때문
- 실제 수치의 integer 근사를 피할 것
- 측정값은 decimal number, count는 integer가 되도록 하자
- fractional quantities는 decimal 값으로 기록하자
3. Character Representations
- 텍스트 데이터의 인코딩 방식을 주의하자
- UTF-8: multibyte encoding for all Unicode characters
4. Name Unification
- 글 저자 기록 방식이 다 다를 수 있음. ex) Steve, Steven. S. 등등
- 이름을 같게 통일하자. 대소문자 변환, 미들네임 제거 등
- false positive와 negative 사이의 tradeoff
5. Time / Date Unification
- 날짜 통일: UTC 등 이용
6. Financial Unification
- Currency conversion: 환율을 이용
- 절대값 변화보다 returns / percentage change를 이용하자
- stock price를 올바르게 하자. (split(액면분할), dividends(배당))
- time value of money는 공정한 장기 비교를 위해 인플레이션의 correction을 해야 한다.
결측치 다루기
- 모른다고 하여 0으로 설정하는 것은 옳지 않다.
- 결측치 처리: 빈칸으로 두는 것보다 estimation, imputation이 필요하다.
Imputation methods
- Heuristic-based imputation: 평균수명을 반영하여 사망일자 예측
- Mean value imputation: 평균으로 대체
- Random value imputation: 난수로 대체 -> 통계적 평가에 imputation의 영향을 줄여줌
- Imputation by nearest neighbor: 가장 가까운 record를 이용하여 대체
- Imputation by interpolation: linear regression을 이용하여 대체 -> record에 빈 필드가 많이 없을 때
Outlier Detection
- 최댓값, 최솟값을 잘 확인하기
- Normally distributed data는 큰 outlier를 갖지 않는다. (k sigma from the mean)
- 그냥 삭제하지 말고 이상치가 생긴 이유를 생각하여 고치기
- 시각화를 통해 탐지하기 쉬움 (저차원인 경우만 가능)
- 클러스터링 했을 때 중심으로부터 멀리 떨어져있는 경우
Delete Outliers Prior to Fitting?
- 적합 이전에 이상치를 지우는 것은 더 나은 모델을 만들어내기도 한다.
ex) 이상치가 측정 오류로 생긴 것일 때
- 반대로 더 나쁜 모델을 만들어내기도 한다.
ex) 간단한 모델에 의해 설명되지 않는다고 해서 해당하는 점을 모두 지워버릴 경우