Probability
- experiment: 가능성이 있는 결과 한 세트를 만들어내는 과정
- sample space S: experiment의 가능성있는 결과의 세트
- event E: experiment의 특정 한 가지 결과
- p(s): probability of an outcome s
0 <= p(s) <= 1 // p(s)의 합 = 1을 만족하는 숫자 -> 확률
- probability of an event E: experiment의 결과들의 확률의 합
P(E) = p(s)의 합 = 1 - p(E^C)
- random variable V: 확률공간의 결과에 대한 numerical function
- expected value of a random variable V
E[V] = p(s) * V(s)의 합
Probability vs. Statistics
- 확률은 미래 사건에 대한 가능성을 예측하는 것을 다룸
- 통계는 과거 사건의 빈도에 대해 분석, 실제 세계에 대한 관측을 합리화하는 데 사용됨
Compound Events and Independence
- independent (독립): 다음 조건을 만족하는 event 2개
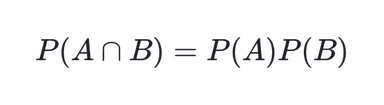
Conditional Probability P(A|B)
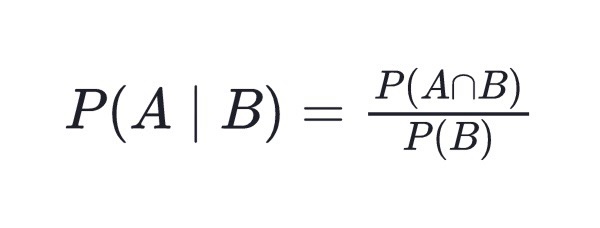
- 정의: B사건이 일어났을 때 A사건도 일어날 확률
- A와 B가 독립일 때, P(A|B) = P(A)
Bayes Theorem
- 의존관계의 방향을 바꿀 때 이용
- 사전확률로부터 사후확률을 구할 수 있음
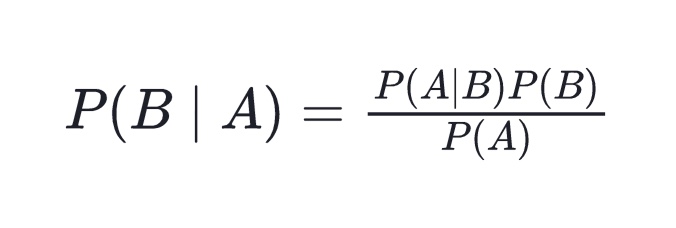
Ex) B: 스팸 이메일인 사건 / A: 이메일인 사건
받은 이메일이 스팸 이메일일 확률을 구할 때 이용
- P(A), P(B)는 각각의 사건의 사전확률이다.
- 사후 확률을 구하기. 어려우므로 approximation ~ naive Bayesian 이용
Distributions of Random Variables
- Random variables: 값과 확률이 같이 등장하는 수치적 함수
- Probability density functions (pdfs): 히스토그램 등으로 RV를 나타냄
- Cumulative density functions (cdfs): running sum of the pdf
- pdf와 cdf는 동일한 정보를 갖고 있다.
- cdf는 성장률에 대한 잘못된 시각을 전달할 수 있다. -> 엄청 빠르게 성장하는 것으로 보이나, pdf로 확인할 경우 개별 연도별 성장률이 그렇게 높지 않을 수 있음.
Descriptive Statistics
- Central tendency measures: 중심점 주변에 분포한 데이터를 설명
- Variation or variability measures: 데이터가 퍼져있는 정도를 설명
Centrality Measure
(Arithmatic) Mean
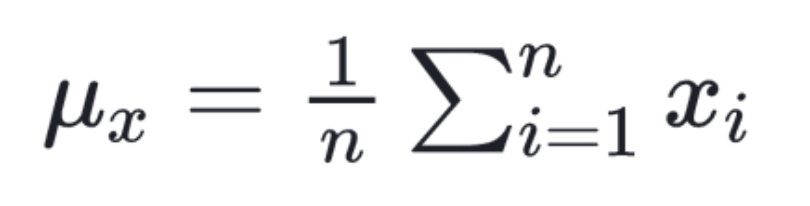
- 장점: outlier가 없는 symmetric distribution에서 의미 있게 사용 가능 (ex. 키, 몸무게 등의 정규분포)
median: middle value
- skewed distribution
- outlier가 있는 데이터
- 부, 수입 등
mode: 가장 자주 나타나는 요소
- 중앙에 가깝지 않을 수 있다.
geometric mean: nth root of the product of n values
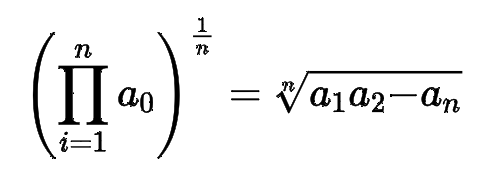
- geometric mean은 항상 arithmetic mean보다 작거나 같다.
- 0에 가까운 값들에 더 민감하다.
- ratio의 mean을 구할 때 사용
Aggregation as Data Reduction
- feature의 개수가 아닌 그냥 데이터의 수를 줄이는 것
- train, test set 나눌 때 유의하지 않으면 편향될 수 있음.
Variance Metric: Standard Deviation
- Variance: standard deviation sigma의 제곱
- population SD: n으로 나눔
- sample SD: n-1로 나눔
- n이 아주 커지면 n ~ (n-1) 이므로 큰 문제가 되지 않음
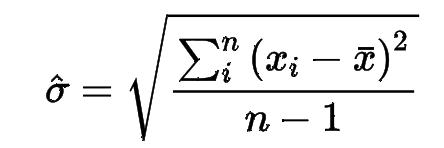
- hat: sample을 의미함
- 평균과 표준편차를 가지고 분포를 특정지을 수 있다.
Parameterizing Distributions
- 데이터가 어떻게 분포해있는지와는 상관없이, 최소한 1-1/k^2번째 점은 평균의 k sigma 안쪽에 있어야 한다.
- 최소한 75%는 평균의 2 sigma 안쪽에 있다.
- Power law의 경우에는 큰 의미가 없다. (skewed data)
- signal to noise ratio를 측정하는 것은 어렵다. -> sampling error, measurement error에 의한 정확하지 않은 분산
Batting Average - Interpreting Variance
- 3할 타자여도, 2할 7푼 5리 이하의 성적을 보일 가능성이 10%나 되고, 3할 2푼 5리 이상의 성적을 보일 가능성도 10%나 된다.
Correlation Analysis
- correlation coefficient r(X, Y): Y가 X의 함수인 정도를 측정한다.
- -1~1사이의 값을 갖는다.
-1: anti-correlated
1: fully-correlated
0: uncorrelated
Pearson Correlation Coefficient
- 분자 = covariance
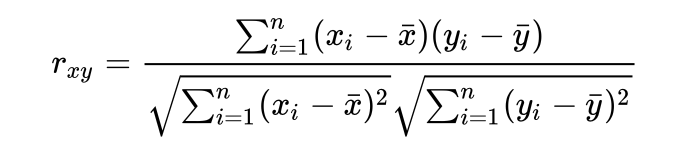
r^2
- X에 의해 설명되는 Y의 비율을 나타낸 지표
Variance Reduction & r^2
- good linear fit f(x)가 있을 때, 잔차 d = y - f(x)는 y에 비해서 더 낮은 분산을 보일 것이다.
- 1-r^2 = V(d)/V(y)
- ex. r = 0.94일 때, 88.4%의 V(y)를 설명할 수 있다.
Significance
- 얼마나 유의하냐~
- sample size, r 모두 중요함
- p value < 0.05 (우연히 보았을 확률이 5% 미만이다)
- 작은 상관관계도 sample size가 충분히 크면 유의해질 수 있음
- permutation test: X를 두고 Y를 섞어서 계산 -> 만번 계산 후 우리가 궁금한 r(X, Y)가 상위 몇 % 안에 있나 확인하는 방법
Spearman Rank Correlation
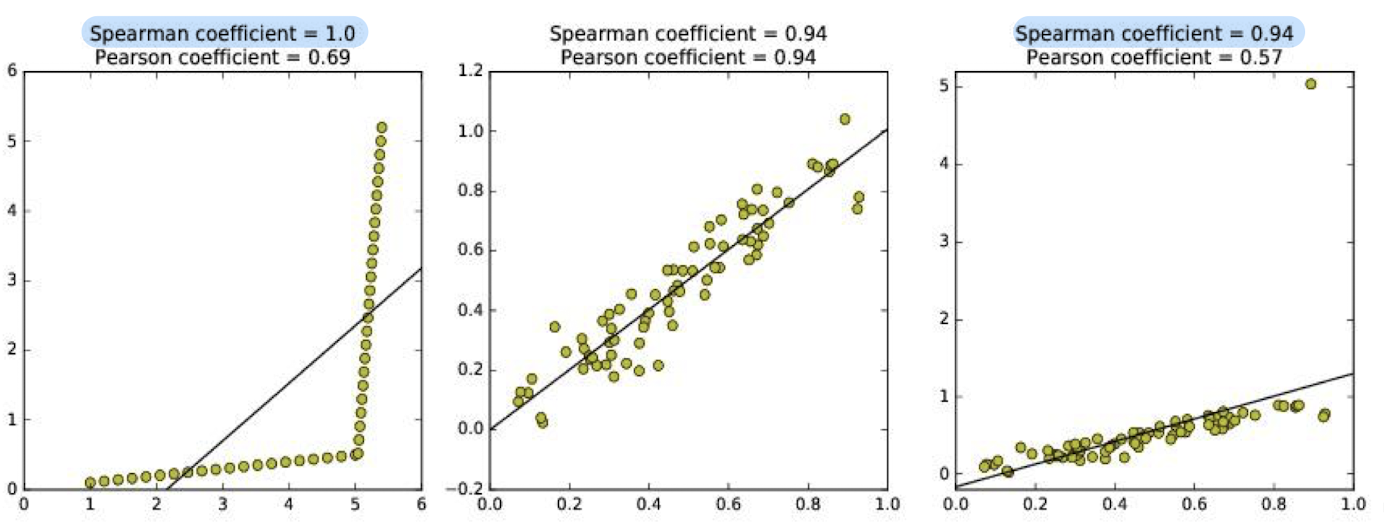
- disordered pair의 수를 세는 방법
- 데이터가 직선에 얼마나 잘 맞는지 확인하는 것이 아님
=> non-linear relationship, outlier에 강점
- 계산 방법
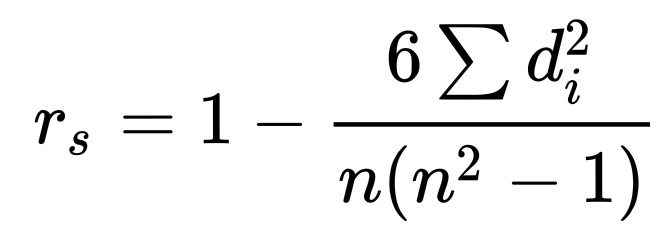
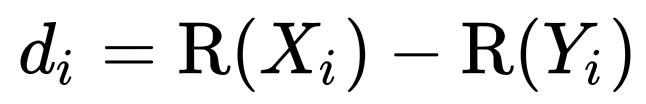
- Pearson correlation rank이므로 범위가 -1~1 사이
Correlation vs. Causation
- Correlation이 causation인 것은 아니다.
- causation: 원인->결과인 방향이 있는 정보
Autocorrelation and Periodicity
- time-series data 중 종종 cycle을 보이는 데이터
- lag-k autocorrelation 계산은 O(n)이지만, Fast Fourier Transform(FFT)를 이용하면 O(nlogn)에 계산 가능
- shifting을 이용하여 correlation을 파악 = 즉, 주기성 파악
Logarithms
- 정의: inverse exponential function
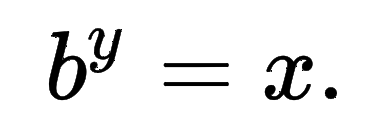
- 컴퓨터의 연산 문제 떄문에 logarithm을 이용하는 것이 더 효율적이다.
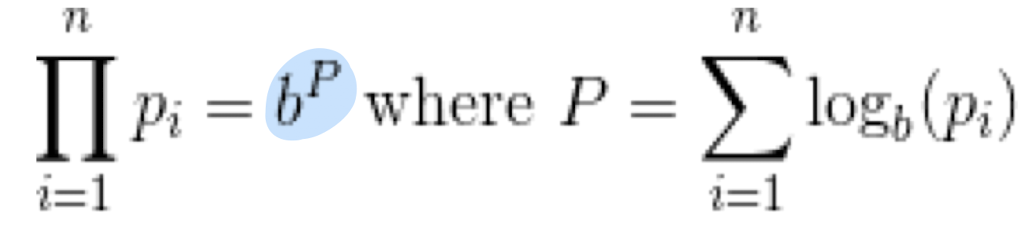
- 비율을 그냥 비교하는 것은 엄청난 차이를 보일 수 있으나 비율에 로그를 취해서 비교할 경우 equal displacement를 보인다.
- power law에서 로그를 씌워서 비교하는 이유.
Normalizing Skewed Distributions
- logarithm을 이용: power law, ratio 등에 이용하여 정규화 가능





