Linear Regression
- n개의 점이 주어졌을 때, 가장 근사를 잘 하거나 잘 맞는 직선을 찾는 것
Error in Linear Regression
- residual error: 예측값과 실제값 사이의 차이
- Least squares regression은 모든 점의 잔차의 합을 최소화함.
-> nice closed form, 부호 무시하므로 선택됨

Contour plots - gradient descent
Linear function을 사용하는 이유
- 이해하기 쉬움
- default model에 적합
* 일한 시간에 따라 급여가 증가 / 지역이 커짐으로써 선형적으로 집값이 상승 / 먹은 음식에 따라 몸무게가 선형적으로 증가
변수가 여러 개일 때
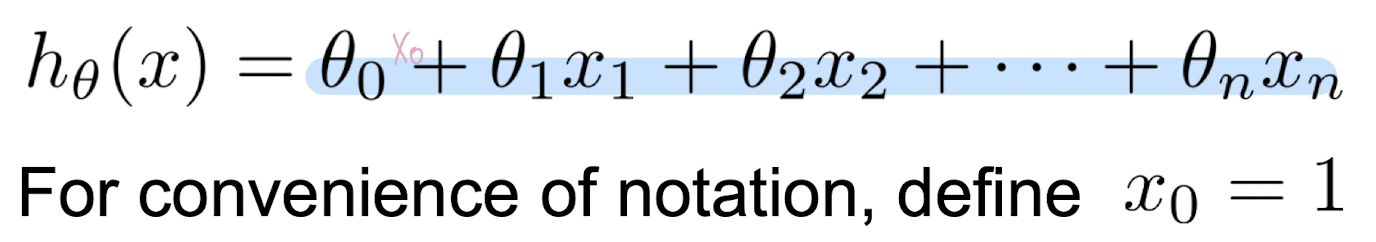
- 각각의 x_n 변수들과 y값을 행렬로 나타내어 세타 값에 대한 행렬을 구할 수 있다.
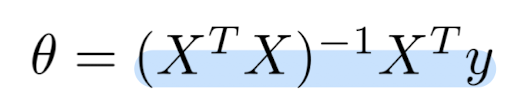
더 나은 회귀 모델
1. 이상치 제거
- 잔차의 quadratic weight 때문에 이상치는 회귀 모델의 fit에 영향을 줄 수 있다.
- 이러한 잔차를 제거하는 것은 더 적합한 모델을 만들 수 있다.
2. nonlinear function fitting
- 기본적으로 Linear regression은 직선이지만, x^2, sqrt(x) 등을 이용하면 곡선을 만들 수 있다.
- 임의로 polynomial, exponential, logarithm 등을 적용할 수 있다.
cf) 딥러닝은 raw feature에서 스스로 원하는 것을 뽑아낼 수 있어 feature engineering에 대한 수요가 적다. 최근에는 prompt engineering을 중요하게 여긴다.
3. feature/target scaling
- 넓은 범위의 데이터를 다루게 되면 coefficient가 지나치게 커질 수 있다.
- Z-score 등으로 스케일을 조정할 필요가 있다.
- power law이 적용되는 수입 등의 데이터에서는 특히 중요하다.
- x값을 log(x), sqrt(x) 등으로 대체할 수 있다.
- feature가 정규분포 형태라면, power law distribution을 갖는 데이터는 linear한 조합으로 나타내기 어렵다.
- Z normalization으로 변형된 데이터를 학습한 후, 결과는 원래 상태로 돌려둔 후 나타내면 된다.
4. highly correlated variable 제거
- 두 데이터가 서로 상관관계가 높다면 더 이상 우리에게 줄 수 있는 정보가 없다. 오히려 혼란을 가중시킴.
--> 따라서 제거해도 된다.
- covariance matrix를 생성하여 제거해야 하는 feature를 찾을 수 있다.
Closed form solution의 문제
- 세타 값을 구하는 방법은 큰 데이터에서는 연산 속도가 엄청 느려진다. - O(n^3)
- linear algebra는 다른 공식에 적용하기 어렵다.
- gradient descent 방식을 선택하게 만든다.
Lines in Parameter Space
- error function J는 convex하다.
Gradient Descent Search
- convex: 1개의 local/global minima 를 갖는 공간
- convex한 공간에서는 minima를 찾기 쉽다. -> 그냥 경사를 따라서 내려가기만 하면 찾을 수 있다.
- 어떤 점에서 내려가는 방향을 찾는 방법은, 미분을 해서 tangent line을 따라 가면 됨
--> (x+dx, f(x+dx))점을 찾은 후, (x, f(x)) 점에 fit

Batch Gradient Descent
- Batch: 각각의 경사하강에서 모든 training sample을 사용하는 것
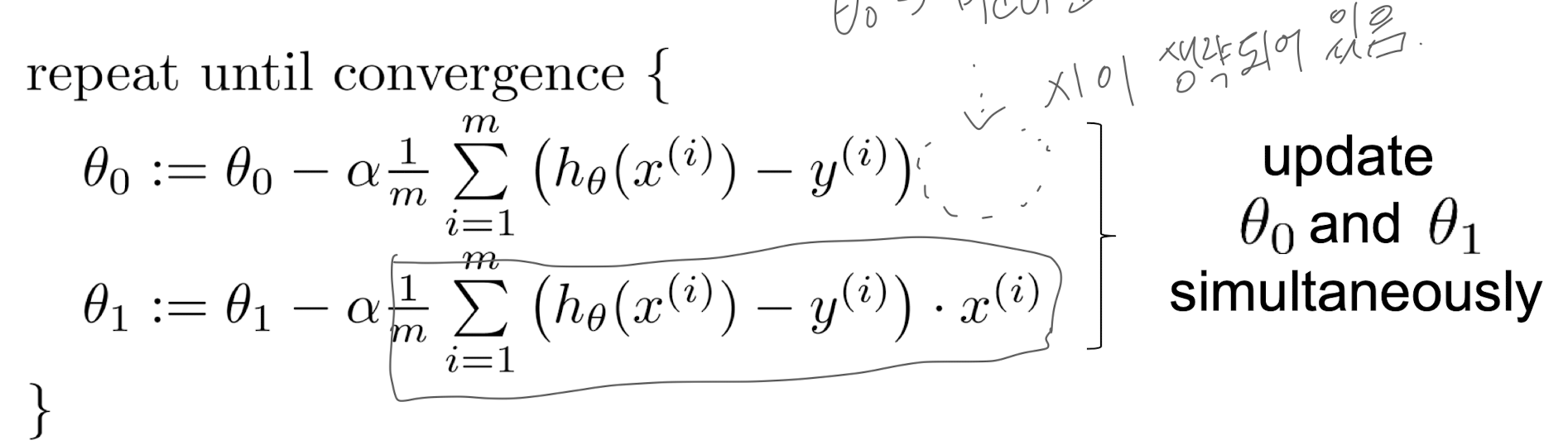
- 통상적으로는 batch size를 줄여가며 경사하강
Local Optima
- J가 convex가 아니라면, 경사하강법을 따라 갔을 때, Local optima에 빠져버릴 수 있다.
Effect of Learning Rate / Step Size
- 너무 작은 스텝으로 움직이면 optima에 convergence하는 속도가 늦다.
- 너무 큰 스텝으로 움직이면 목표에 도달하지 못할 수 있다.
- 적절한 step size를 구하려면?
-> step size가 적절한지 판단하고, 너무 늦다면 multiplicative factor (3의 지수배 등등) 를 이용하여 늘려보기
-> 너무 크다면 (1/3의 지수배 등) 줄여보기
Stochastic Gradient Descent
- batch size도 hyperparameter이다.
- 모든 example이 아닌 일부만 이용하여 derivative를 계산하는 것도 방법
Regulation
- J 함수에 coefficient가 작게 유지되도록 람다 값을 추가

- 람다 값이 0에 가까워지면 error는 감소하고, 무한대에 가까워지면 thetha_0만 식에 남게 된다.
- 데이터에 최대한 가깝게 식을 만들면 error는 감소하지만, 위 공식에서 파란 부분은 커진다.
Interpreting/Penalizing Coefficients
- Squared coefficient의 합을 Penalizing 하는 것은 ridge regression or Tikhonov regularization
- coefficient의 절댓값을 penalizing하는 것은 LASSO regression이다.
* L1 metric
* L2: 각 차원에 대한 제곱의 합 -> 유클리드 거리
LASSO (Least Absolute Shrinkage and Selection Operator)
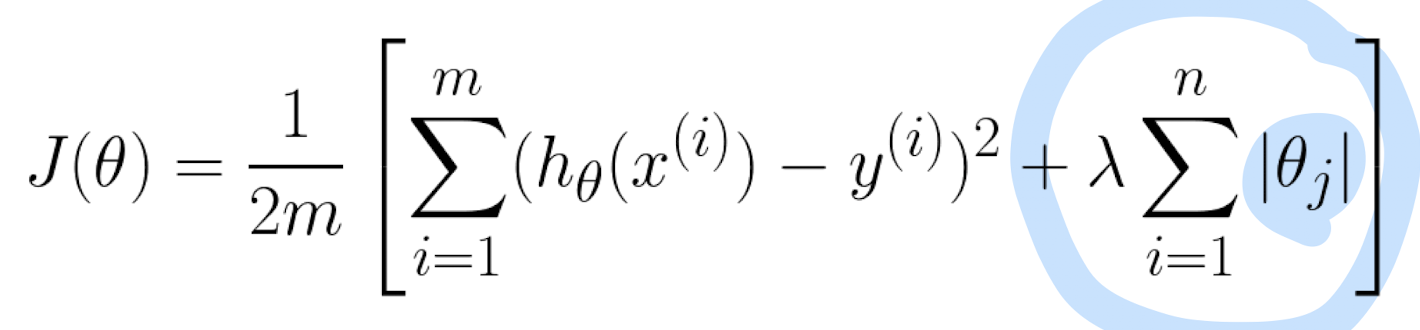
- sparse solution을 선택하는 경향
- 변수 선택 및 regularization 기능
- interpretability를 향상
What is right Lambda?
- 람다가 커지면 small parameter를 강조 -> ex) set to all zeros
- 람다가 작아지면 training error 를 줄이기 위해 모든 파라미터를 자유롭게 이용할 수 있음
- 오버피팅/언더피팅 사이 균형을 유지해야 함
Normal form with regulation
- Normal form equation은 regularization을 다루기 위해 일반화될 수 있다.
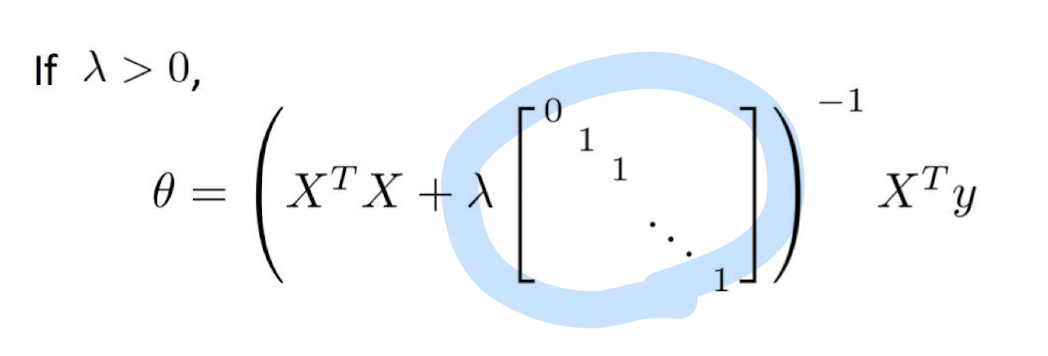
- 또는 경사하강을 이용할 수도 있다.
Classification
- 분류는 남자/여자, 스팸/일반메일, 악성/양성 종양 등의 구분에 이용
- input record에 라벨을 부여
Regression for Classification
- linear regression을 이용하여 분류 문제를 해결할 수 있다.
- 이때 각각의 분류에 대해 0/1의 이진 분류를 사용한다.
- positive = 1, negative = 0
- regression 선은 이러한 분류를 나눌 것이다.
- 극단적인 +, - 사례를 추가할 경우 선이 바뀐다.
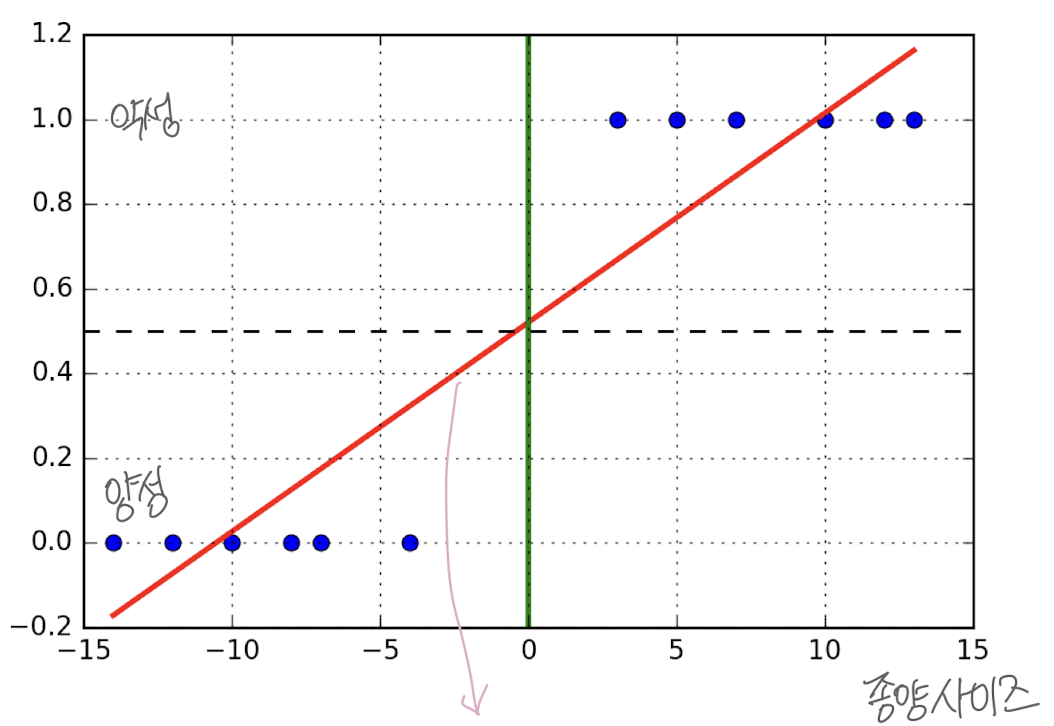
Decision Boundaries
- Feature space에서 선을 통해 클래스를 분류할 수 있다.
- Logistic Regression: 가장 적합한 분류 선을 찾기 위한 방법
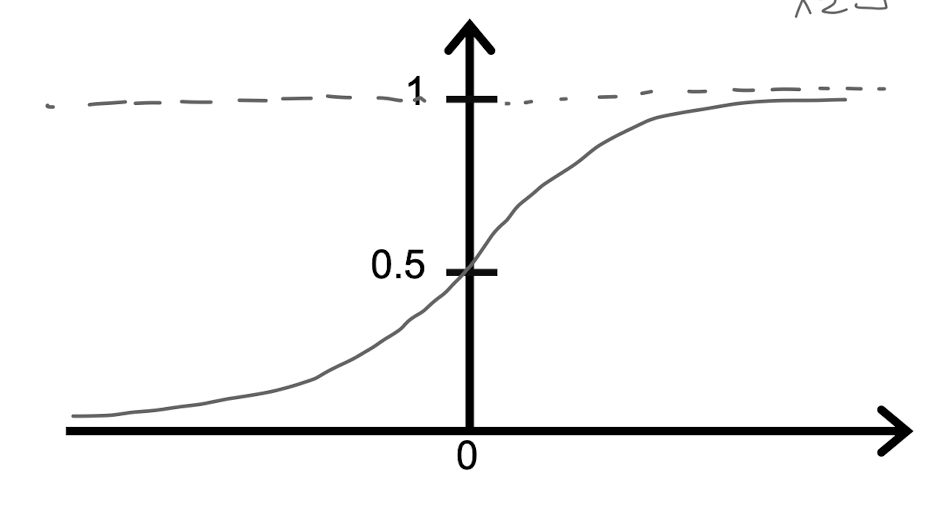
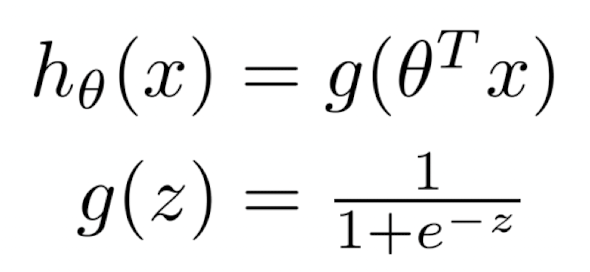
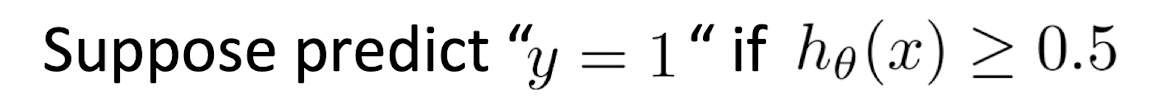
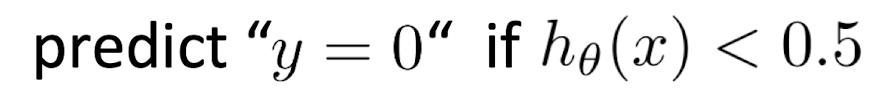
Cost for Positive/Negative Cases
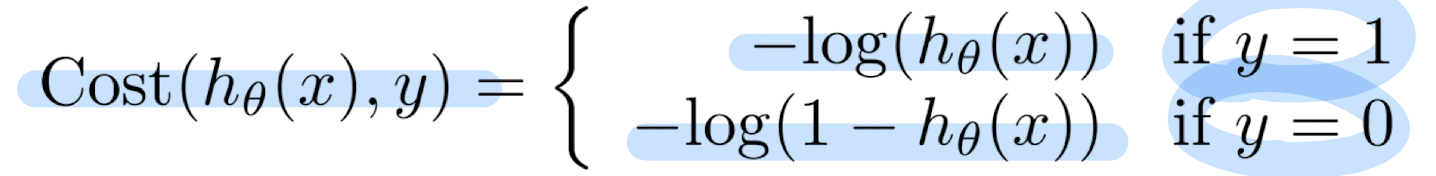
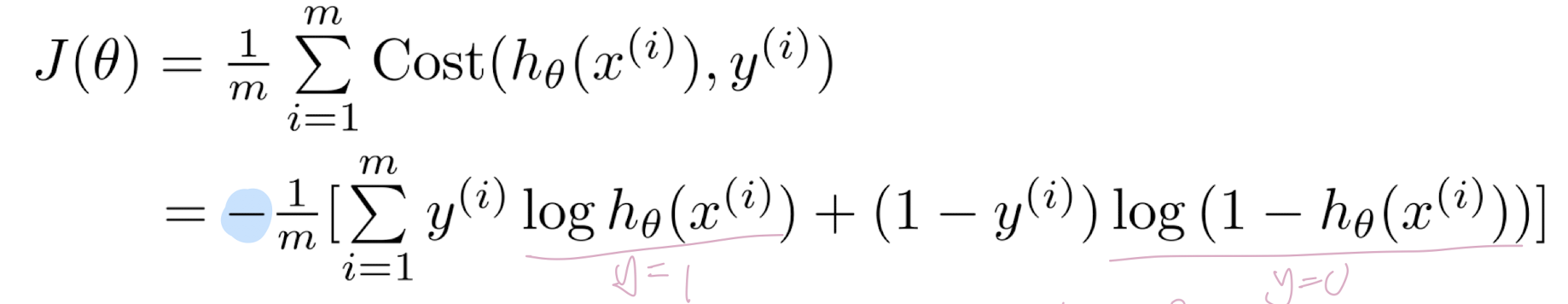
- 세타 값을 줄이는 것이 목표임
- 새로운 x에 대한 예측
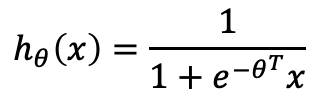
Logistic Regression via Gradient Descent
- loss function이 convex하므로, 경사 하강을 통해 가장 적합한 파라미터를 찾을 수 있다.
-> 따라서 두 클래스에 대한 linear seperator를 찾을 수 있다.
Logisitc Gender Classification
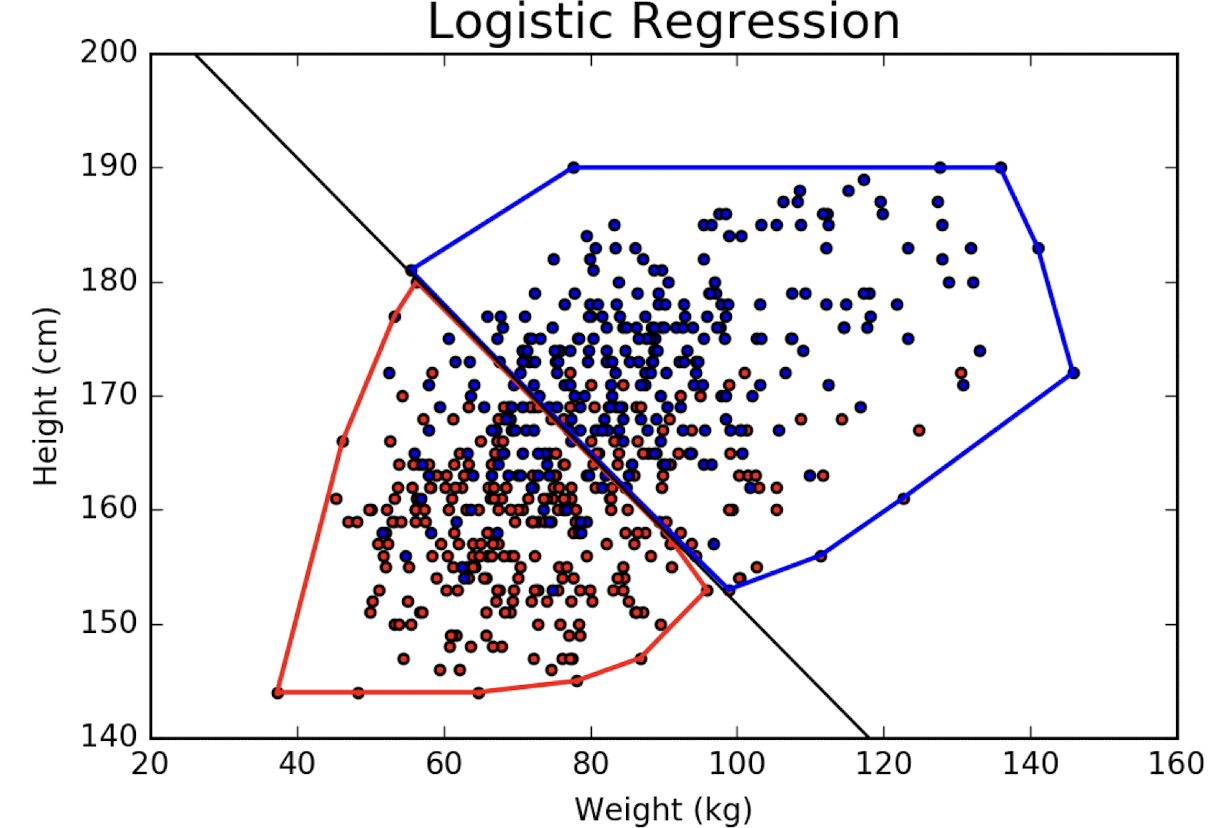
Classification의 문제
1. Balanced Training Classes
- 긍정 라벨을 가진 데이터가 1개고 부정 라벨을 가진 데이터가 10만개 있다면 올바른 결과가 나올 수 없다.
- 각각의 라벨 데이터 수를 맞추자.
* minority class에 해당하는 데이터를 찾기 위해 더 노력하기
* 더 큰 class의 요소를 버리기
* minority class에 가중치 부여 -> overfitting 조심하기
* small class에 대해 데이터를 복제하기 -> random perturbation (복원추출로 여러개 뽑아서 앙상블 진행)
2. Multi-Class Classifications
- 모든 분류가 이진적이지는 않음.
- ordering 관계가 없는 분류에 대해서는 단순히 숫자로 표현하여 분류를 진행하면 안 된다.
- ordinal data에 대해서만 숫자로 라벨링 가능. 아닌 경우 원 핫 인코딩 이용.
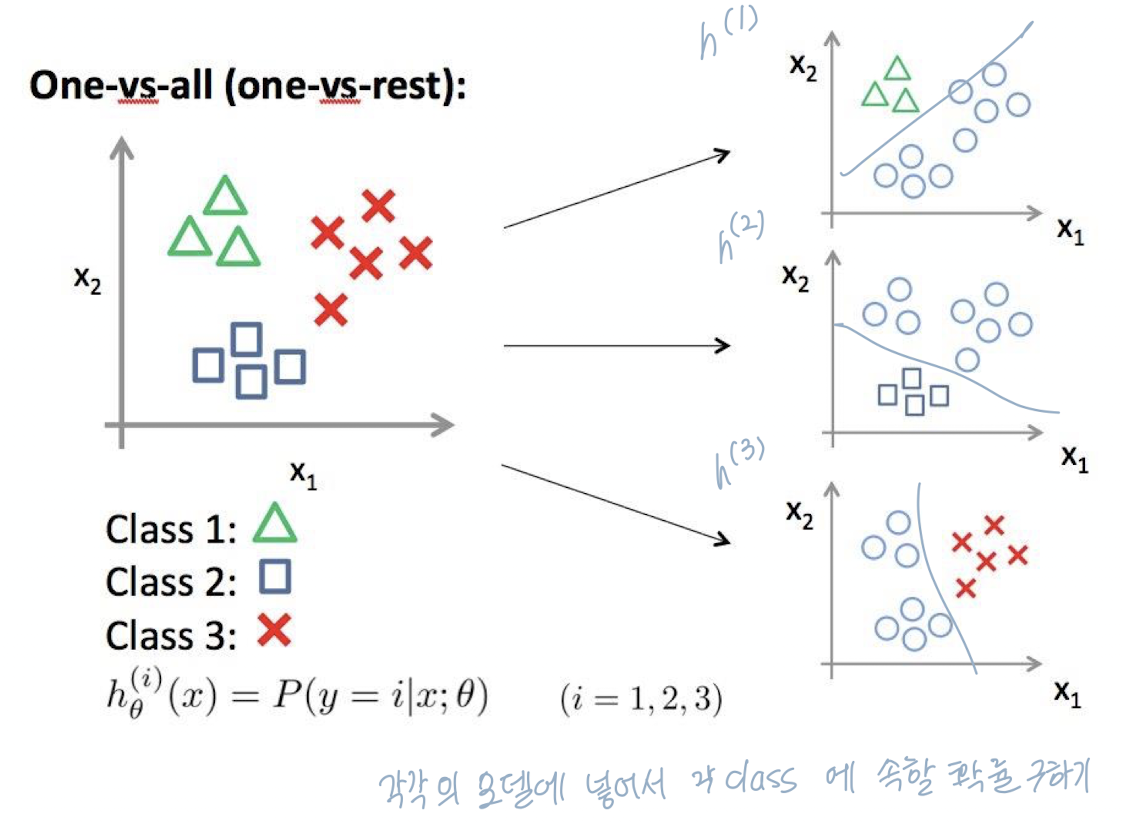
cf) One Versus All Classifiers
- 다중 독립 이진분류기를 이용하여 multiclass classifier를 만들 수 있다.
- 각 분류기가 예측한 가능성 중 가장 큰 것을 채택.
3. Hierarchical Classification
- 유사성을 이용해 그룹으로 나누고 taxonomy를 만드는 것은 효율적인 class 개수를 줄일 수 있게 한다.
- top-down tree를 이용해 분류






