Chapter 8. Linear Algebra

Linear Algebra / 선형대수학

- matrix의 수학

- 데이터 과학에서 중요한 역할

 

n * m matrix가 나타낼 수 있는 것

	row	column
Data	object	features
Geometric Point Sets	point	dimensions
Systems of equations	equations	각 변수의 coefficient

- Graphs/Networks: M[i, j] = vertex i -> vertex j edge 개수

- Vectors: any row, column or d*1 matrix

 

Vector 사이의 각 

- 벡터 A와 B 사이의 각도

- cos(0) = 1 ---> perfect similarity = 0

- cos(pi/2) = 0 ---> 관련이 없다

- cos(pi) = -1 ---> perfect anticorrelation

==> cos = correlation of mean zero variables

- unit vector에 대해서 그 벡터의 크기는 1이므로, dot product로 정의된다.

 

Transpose

- 정의: a*b matrix -> b*a matrix로 변환하는 것

- addition and transposition

-> B = A^T라고 가정했을 때 합하는 방법

- a 값을 조정할 수 있음.

 

Matrix multiplication & Dot Products

- A*B는 같은 내부 차원을 공유해야만 계산 가능하다.

- 결과행렬의 각 요소는 row/column 벡터의 dot product 

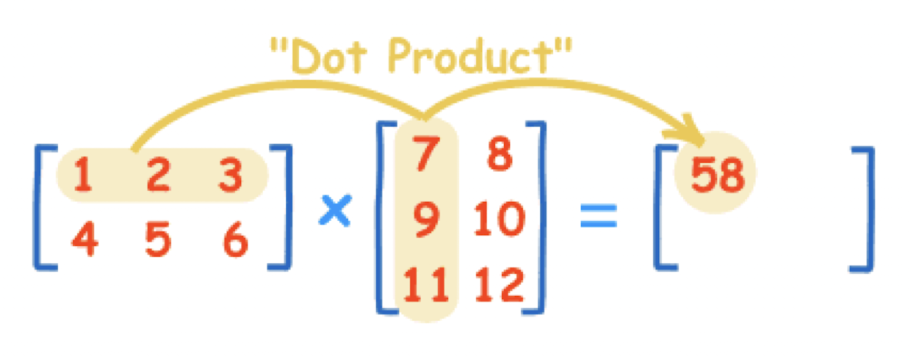
- dot product는 두 개의 벡터가 얼마나 유사한지 측정하는 방법이다.

- 행렬의 곱셈은 결합법칙은 성립하나 교환법칙은 성립하지 않는다.

 

Multiplying Feature Matrices

- 행렬 A가 n*d data matrix라고 가정해보자.

- n: 문서, d: 용어

- C 행렬은 n*n matrix of dot products - 점들 간의 유사도를 나타내는 행렬이 된다.

- D 행렬은 d*d matrix of dot products - 특성 간의 유사도를 나타내는 행렬이 된다.

- covariance matrix 로 해석할 수 있다.

예시) car - automobile : D matrix 계산 후 두 값을 나타내는 cell을 확인해보면 다른 cell보다 값이 높은 것을 확인할 수 있다. - 유사도가 높다.

 

Interpreting Matrix Multiplication

- 0/1 adjacency matrices 를 곱하는 것은 두 점 사이의 거리를 나타내는 행렬이 된다.

- Multiplication by permutation matrices는 행/열을 재정렬한다.

 

Matrix Rank

- 정의: 선형 독립적인 row의 수를 측정하는 것

- n*n matrix는 순위가 n이 되어야 한다.

Rank 1 인 Matrix - 두 식이 사실상 같은 의미이므로 풀 수 없다.

Rank 2인 matrix

* 랭크란 행렬의 열들로 생성될 수 있는 벡터 공간의 차원.

참고문헌: https://blog.naver.com/sw4r/221416614473

[기초 선형대수] 행렬에서 Rank (랭크) 란?

 

2=1 증명으로부터 알 수 있는 것

- 증명에 오류가 생기는 원인: 0으로 나누는 것이 불가능하다는 것을 간과함

- 선형 대수에서 singular matrix도 포함된다.

 

Matrix를 나누는 것

- inverse operation: x를 identity element로 내리는 것

- 곱셈의 inverse는 나눗셈.

- 덧셈의 inverse는 뺄셈.

 

Matrix Inversion

- A^-1 : A * A^-1 = I 인 matrix (I = identity matrix)

- A 행렬이 inverse를 가진다면, Gaussian elimination을 이용하여 계산될 수 있다.

* 가우스 소거법

https://m.blog.naver.com/siri0831/222033492473

선형대수학(1) - 가우스 소거법(Gauss Elimination)

 

Matrix Inversion and Linear Systems

- Ax=b 식에 A의 역행렬 A^-1을 곱하면 다음의 식이 나타난다.

- 선형식의 해를 구하는 것은 matrix의 역행렬을 곱하는 것과 같다.

Principle Component Analysis (PCA)

- 데이터를 2개의 축으로 projection하는 것이다.

- 어떤 기준으로 축을 골라야 할 것인가?

1) 1차원 projection을 했을 때 데이터 분산이 가장 큰 것을 선택한다.

* 이유: 정보 유실을 최소화해야하므로

2) 첫번째 축과 직교하면서 분산이 가장 큰 축을 선택한다. --> 새로운 공간을 만들어낸다.

 

Singular Value Decomposition (SVD) : 특이값 분해

- 이미지 처리 등에 사용됨

- V*, U*는 각 행렬의 역행렬이라고 생각하면 됨

- https://darkpgmr.tistory.com/106

[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용

 

Reconstructing Lincoln