Chapter 5. Statistical Analysis

Central Dogma of Statistics

 

 

Statistical Data Distributions

- 모든 random variable은 특정 빈도/확률 분포를 갖는다.

- 종류: binomial distribution, normal distribution, poisson distribution, power law distribution

 

Classical Distribution의 중요성

- 실제로 사용하는 경우도 있음

- Closed-form formula(cdf, pdf), test(t-test) 등을 이용 가능

- 모양이 비슷하다고 이러한 분포와 같다고 생각하면 안 된다.

 

Binomial Distribution

- n개의 independent trial로 이루어진 실험 -> 2가지의 결과를 가져야 함

- 예: 동전 던지기

- 분포: 이산적이나 종 모양임 (또는 half-bell shape)

 

Normal Distribution

- 종 모양을 가짐

- 키, IQ 등.

- 평균과 표준편차로 나타낼 수 있음.

- 모든 종 모양 분포가 normal distribution은 아니다.

- n이 무한대로 발산하는 binomial distribution

- normal distribution을 갖는 변수들의 합은 normal하다.

- normal distribution의 mixture는 normal하지 않다.

-> 여성의 키, 남성의 키 각각은 정규분포지만, 전체 인구의 키는 정규분포가 아니다.

 

Lifespan Distribution

- 매일매일의 생존 확률이 p라면, n일동안 생존할 확률은 p^(n-1)*(1-p)

 

Poisson Distribution

- rare event에서의 interval의 빈도

 

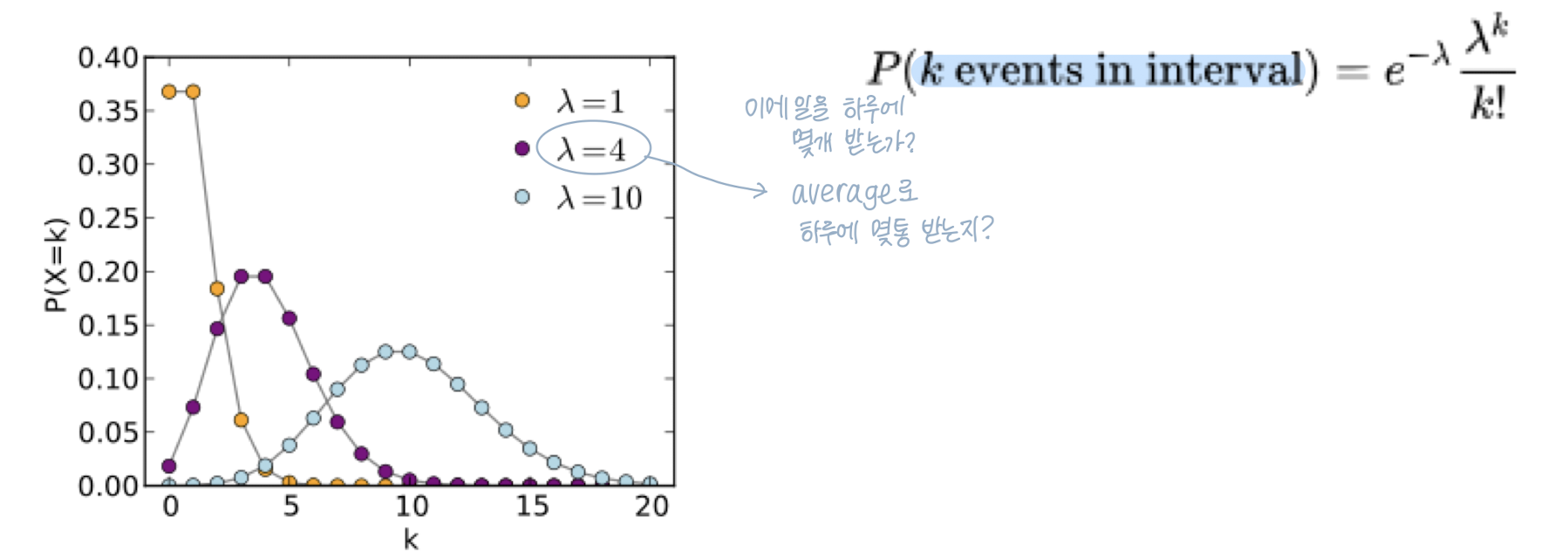
Power law Distribution

- 정의: P(X=x) = cx^(-a)

* c: normalization 상수, a: exponent

* c: a가 주어지면, 확률들의 합은 1이어야 하므로 하나의 값으로 정해진다.

- 정규분포처럼 중앙에 밀집하지 않고 지속적으로 아주 큰 값을 갖는다.

- 80-20 rules: 20%의 X가 80%의 Y를 갖는다. -> 빈부 격차 등에서 소수의 부자들이 부를 독식한다 등등

ex) City Population - Power Law

: 부를 가진 사람이 점점 더 부자가 된다.

- x가 2배가 될 때, 확률은 2^a만큼 줄어든다.

- Power Law의 예시

1) x개의 링크를 가진 인터넷 사이트

2) 리히터 규모와 지진의 빈도

3) 단어 사용 빈도

4) x명을 죽인 전쟁의 수

 

Word Frequencies and Zipf's Law

- Zipf's law: k번째로 가장 인기 있는 단어는 가장 인기 있는 단어의 1/k번째 만큼 사용된다.

-> a = 1인 power law

-> 2x번째인 단어는 x번째 단어의 사용 빈도 * 1/2

 

Power Law의 특성

- 평균은 의미가 없다.

- 표준편차도 의미가 없다. 평균보다 훨씬 큰 값이 있기 때문에

- 중앙값은 의미가 있다.

- 분포는 scale invariant하다 = 확대한 분포의 일부가 전체 분포의 모양과 비슷해 보인다. 

 

통계학자 vs 데이터마이너

- 통계학자: 데이터에서 발견한 것이 중요한지에 관심

- 데이터마이너: 데이터에서 발견한 것이 흥미로운지 관심

- meaningful한 발견: 큰 데이터셋에서 강한 상관관계는 겉으로는 중요해보일 수 있으나, 문제는 더 세밀하게 봐야 할 수 있다.

 

Comparing Population Means

- T-test: 두 샘플의 평균 사이의 차이에 대해 평가

- 평균이 다르거나, 표준편차가 다를 경우 차이를 그냥 판단하기 쉽다.

 

T-test

- 2개의 평균은 상당히 다르다. 어떨 때?

* 평균의 차이가 비교적 클 때

* 표준편차가 충분히 작을 때

* 샘플이 충분히 클 때

- Welch's t-statistic

* s^2: sample variance

- t distribution table

* df: 자유도 (모집단의 개수가 n개일 때 자유도는 n-1이다)

* one tail일 때 t값의 기준이 낮아진다.

* 120일 때 1.98, 무한대로 발산하는 경우 1.96이 된다.

 

Kolmogorov-Smirnov Test (KS-test)

- 두 개의 cdf 사이의 최대 y-distance 차이를 이용해 확률 분포의 차이를 나타냄.

- max distance between two cdfs: D(C1, C2) = max|C1(x)-C2(x)| (-∞ <= x <= ∞)

- 유의수준 a일 때, D(C1, C2) > c(a)* √((n1+n2)/n1n2) 이면 다른 분포이다.

* c(a): table lookup으로 찾을 수 있음

 

Normality Testing

- 이론적인 분포에서 샘플링된 분포에 대해 KS-test를 수행할 수 있다.

 

Bonferroni Correction

- 0.05의 통계적 유의수준은 우연히 이 결과가 나타났을 확률이 1/20이라는 뜻이다.

-> 더 높은 기준으로 평가되어야 하는 이유

- n개의 가설 검정을 할 때, p-value는 a/n 수준이 되어야 한다. -> 그래야 a 수준에서 유의하게 고려될 수 있다.

 

Significance of Significance

- 충분히 큰 샘플 사이즈라면 극도로 작은 차이는 매우 유의하게 여겨질 수 있다.

- significance(유의성)은 분포 사이에 차이가 있다고 확신할 수 있는 정도를 측정하는 것이지, effect size나 importance/magnitude of difference를 측정하는 것이 아니다.

 

Effect Size 측정

- Pearson correlation coefficient: 0.2 = 작은 effect, 0.5 = 중간, 0.8 = 큼

- Percentage of overlap between distribution: 53% = 작음, 67% = 중간, 85% = 큼

- Cohen's d = (u- u')/sigma : small > 0.2, medium > 0.5, large > 0.8

 

Permutation test, p-values

- 데이터로 가설을 입증할 수 있다면, 랜덤하게 섞은 데이터셋으로도 가설이 입증되어야 한다.

- random permutation 사이의 실제 데이터 순위가 significance를 결정한다.

- (최소 1000번 이상-p value가 소수점 세자리까지 나온다) permutation을 많이 수행할 수록, significance가 더 중요해진다. 

알고리즘으로 설명할 경우 다음과 같다.

for i=1 to n do a[i]=i;
for i=1 to n-1 do swap(a[i], a[Random[i,n]);

*Random 함수에서 1~n번째 사이의 데이터를 골라서 섞으면 uniform하게 섞이지 않은 데이터가 된다.

 

Sampling from distributions

- 원형 데이터에서 반지름 길이와 각으로 랜덤하게 데이터를 고르면 중앙에 몰리는 값이 많아진다.

- (x, y)로 데이터를 찍어야 한다.

 

Sampling in One dimension

- 어떠한 확률분포에서든 샘플링을 하려면 cdf 형태로 바꿔서 추출하면 된다.

 

Statistical Hypothesis Testing

Central Limit Theorem

- random variable: 독립적이고 동질적으로 분포된 큰 수의 평균 (i.i.d.)

- random variable은 정규분포 되어있다고 근사할 수 있다.

- x1, ..., xn이 μ, σ^2로 된 random variable이고 n이 엄청 크다면

Z = 1/n * (x1+...+xn)은 근사적으로 정규분포를 갖는다. (평균 μ, 표준편차 σ^2/n)

- n이 엄청 커지면 Binomial(n, p)~Normal(np, np(1-p))으로 근사 가능하다.

(n 번의 독립적인 베르누이 시행의 합으로 된 랜덤 변수)

- 중심 극한 정리의 중요성: 다른 형태의 분포를 포함한 문제를 정규분포 형태로 적용 가능

 

Statistical hypothesis testing

동전 던지기에서 동전의 양면이 공평하지 않을 때를 가정해보면,

H0 (귀무가설, null hypothesis): 동전은 공평하다. == p=0.5이다.

H1 (대립가설, alternative hypothesis): 동전은 공평하지 않다. -> 우리가 입증하고 싶은 것

 

검증하는 방법은 다음과 같다.

- 동전을 n번 던져서 앞면이 나오는 횟수를 센다.

- 매번의 동전 던지기는 Bernoulli trial이므로, X는 Binomial(n, p)이다.

- CLT에 의해 X는 Normal(np, np(1-p))로 근사될 수 있다.

- 유의 수준을 결정: 1종 오류 (False Positive) 를 허용할 범위

- 유의수준을 0.05로 결정했다고 했을 때, 만약 앞면이 532번 나왔다고 하면, 4.63%에 속하는 범위이다. -> 유의한 수준의 결과이므로 H0을 기각하고 H1을 채택한다.

 

Error의 종류

		귀무가설의 참/거짓 여부
		참	거짓
H0(귀무가설)에 대한 판단	기각 (positive call)	1종 오류 (False Positive)	정답 (True Positive)
	기각 실패 (negative call)	정답 (True Negative)	2종 오류 (False Negative)

Statistical Hypothesis Testing with p-value

- P-value: 확률(귀무가설(H0)이 옳다고 판단)

- 일반적인 경우 유의수준은 0.05 또는 0.01로 설정

- X = 530 일 때, p-value = 0.062, X = 532일 때 p-value = 0.0463

 

Confidence interval : 신뢰구간

1000번 중 529번 앞면을 보았을 때, p=0.529이다.

p_hat = 0.529
sigma_hat = math.sqrt(p_hat*(1-p_hat)/1000)
print normal_two_sided_bounds(0.95, p_hat, sigma_hat) # 0.95 = 유의수준

>>> [0.498, 0.560]
# 실제 p는 이 구간 안에 95% 확률로 존재한다.

 

Example: Running an A/B test

- 2개의 광고 중 클릭을 더 많이 유도하는 광고를 선택해야 함.

- Na = A 광고를 보는 사람의 수, na = A 광고를 클릭하는 사람의 수, pa = A 광고를 클릭할 확률

-> na/Na는 Normal(pa, pa(1-pa)/Na)로 근사될 수 있다. (이유: 베르누이 시행을 n 번 반복한 것이므로)

-> nb/Nb는 Normal(pb, pb(1-pb)/Nb)로 근사될 수 있다.

- 2개의 분포는 독립적이므로 두 개의 차이도 normal 해야 한다.

- H0을 pa=pb라고 가정해서 검정할 수 있다.

- 유의수준을 0.05라고 가정하고 해보자.