Heap의 개념
힙은 트리의 일종인데, "complete tree"이거나 "nearly complete tree"이어야 한다. 그리고 다음 두 가지 종류로 나뉜다.
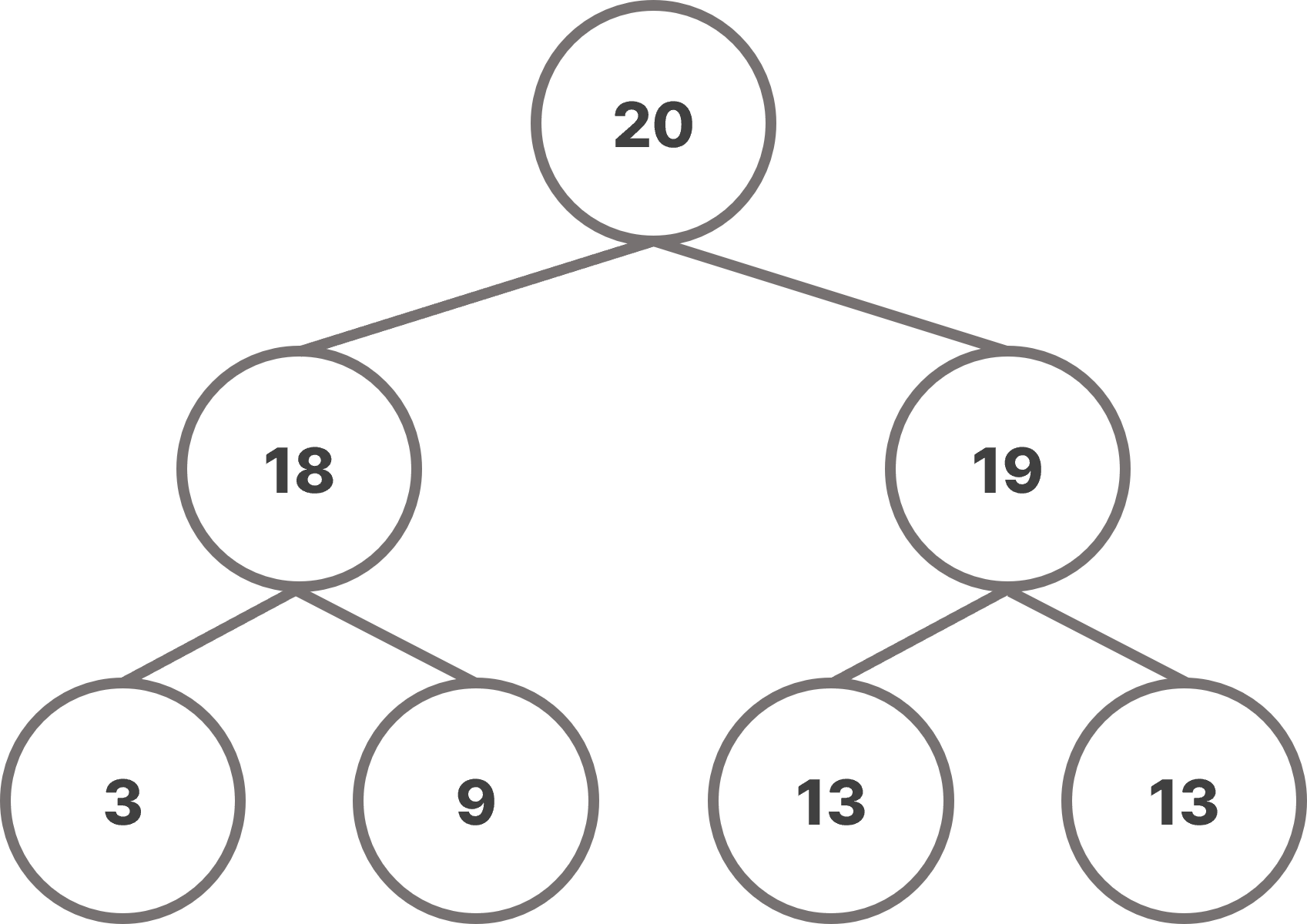
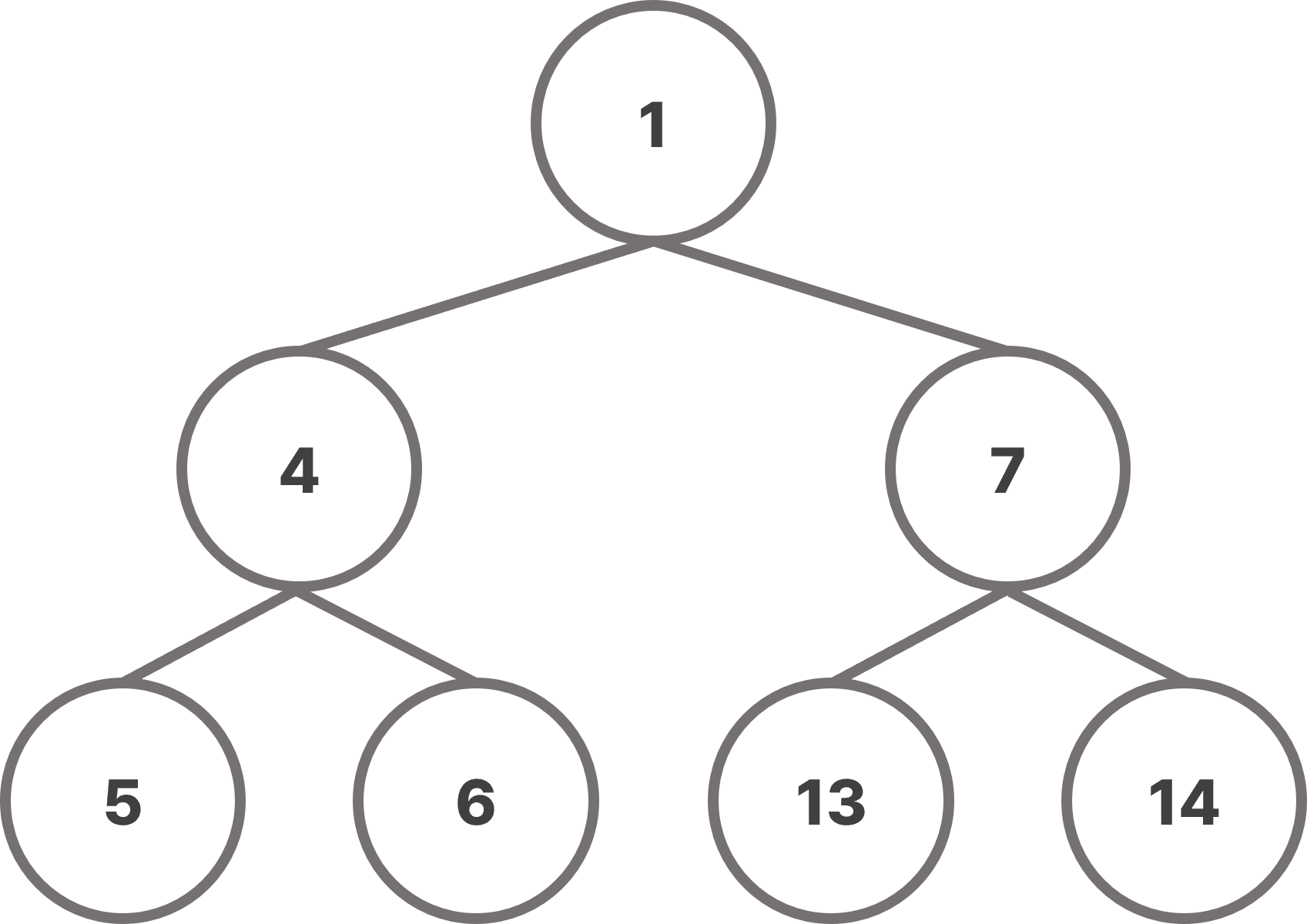
max-heap의 경우 각 노드의 key 값이 자식 노드들의 key 값보다 크거나 같고, min-heap의 경우 각 노드의 key 값은 자식 노드들의 key 값보다 작거나 같아야 한다.
Heap의 특성
max-heap을 기준으로 살펴보자. 힙의 root는 트리에서 가장 큰 값을 갖고 있으며, root의 왼쪽/오른쪽 서브트리도 같은 특성을 유지한다. 만약 min-heap이라면 힙의 root가 트리에서 가장 작은 값을 갖게 된다.
구현은 주로 linked list보다는 array로 이루어진다.

노드와 자식 간의 관계는 다음과 같이 확인할 수 있다.
index가 i인 노드를 생각해본다면,
-
- i번째 노드 왼쪽 자식: 2i+1
- i번째 노드 오른쪽 자식: 2i+2
- i번째 노드의 부모 노드: floor((i-2)/2)
- j번째 노드가 왼쪽 자식이면, 오른쪽 자식은 j+1
Heap의 연산
Heap에서 자료를 추가하거나 삭제할 수 있으며, 순회, 검색, 출력과 같은 기능도 작동하게 할 수 있다.
다만 힙은 위에서 언급한, root의 key 값이 가장 크거나 (max-heap) 작아야 (min-heap) 하고 그 특성이 모든 서브트리에 대해서도 동일하게 유지되어야 하며, 정의했던 것처럼 (nearly) complete tree라는 특성도 유지해야 한다.
만약 노드를 추가하거나 삭제를 한 후 그냥 가만히 둔다면 힙의 정의를 만족하지 못할 것이다.
따라서 우리는 Reheap up / Reheap down 이라는 함수를 정의해서 heap의 모양을 유지하도록 한다.
수도코드의 경우, 순회, 검색, 출력 자체는 기존 트리에서 구현하는 것과 동일하므로 건너뛰고, 삽입 및 삭제의 경우는 각각 함수의 뒷부분에서 Reheap up, Reheap down함수를 불러오기만 하면 되므로 건너뛰도록 하겠다. 여기에서는 Reheap Up 및 Reheap Down에 대해서만 소개하도록 하겠다.
Reheap Up
삽입 연산을 수행하면서 같이 불러와야 하는 함수로 가장 마지막에 삽입된 요소를 위쪽으로 이동시키면서 올바른 위치에 갈 수 있게 한다. 삽입 자체는 가장 첫 번째 빈 leaf node에 들어가기 때문에 heap의 구조를 유지하기 위해서는 node를 이동시켜주어야 한다.
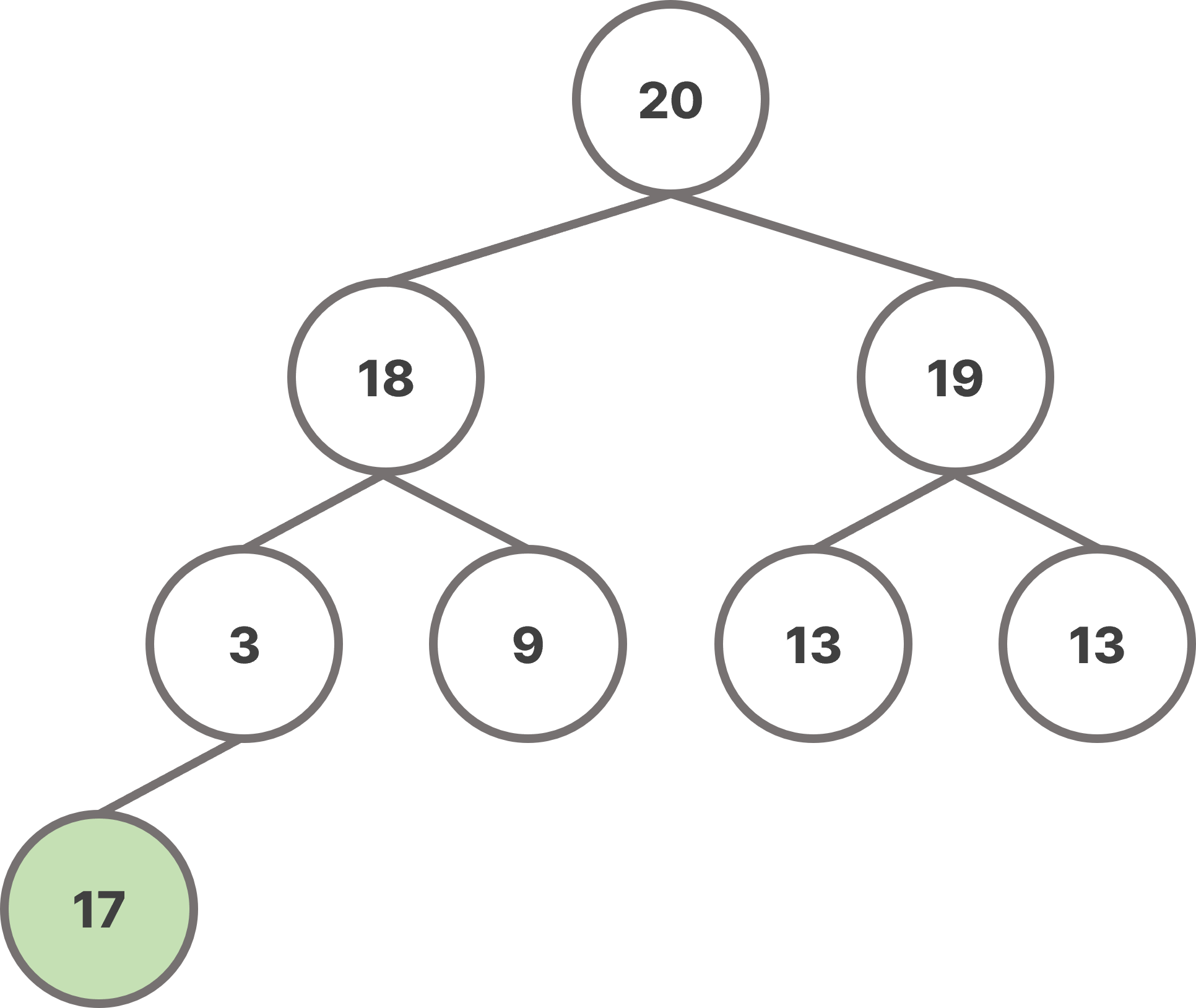
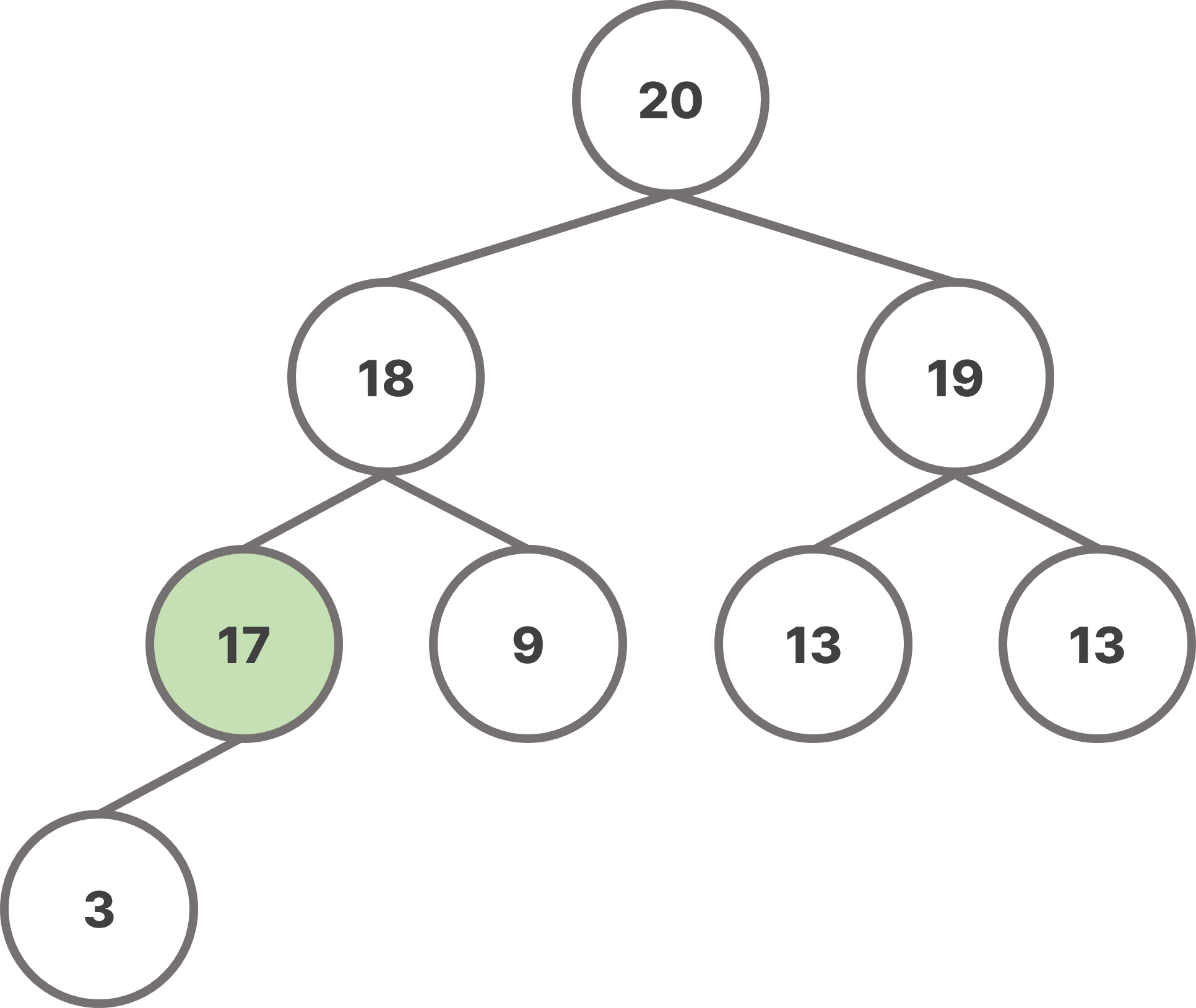
삽입된 노드의 부모 노드와 key 값을 비교하여, 만약 삽입된 노드가 부모 노드의 key 값보다 크면 서로 위치를 교환한다. 이 과정을 계속 반복하여 heap의 구조를 유지시킨다.
수도코드는 다음과 같다.
void reheapUp (HEAP *heap, NODE *newNode) {
if (newNode != root) {
parent = parent->newNode;
if (newNode->key > parent->key) {
swap(newNode, parent);
reheapUp(heap,parent);
}
}
}
Reheap Down
heap은 nearly complete tree이므로 root을 바로 삭제하게 되면, heap의 구조가 유지되지 못한다. 따라서 last tree node의 값을 root로 옮긴 후, root를 아래로 이동시켜서 heap의 배열 특성(heap-ordering property)이 충족되도록 위치를 변경해야한다.
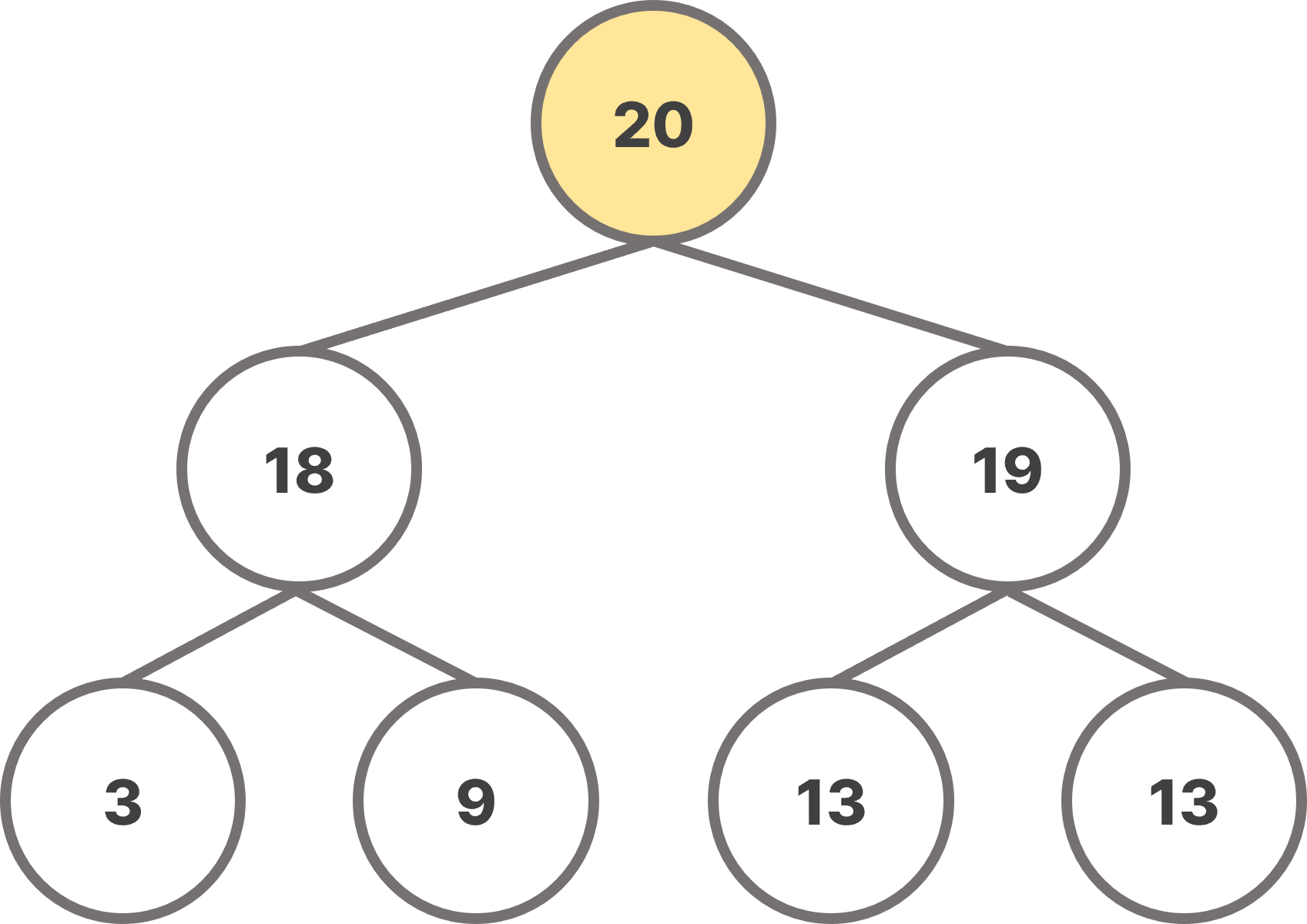
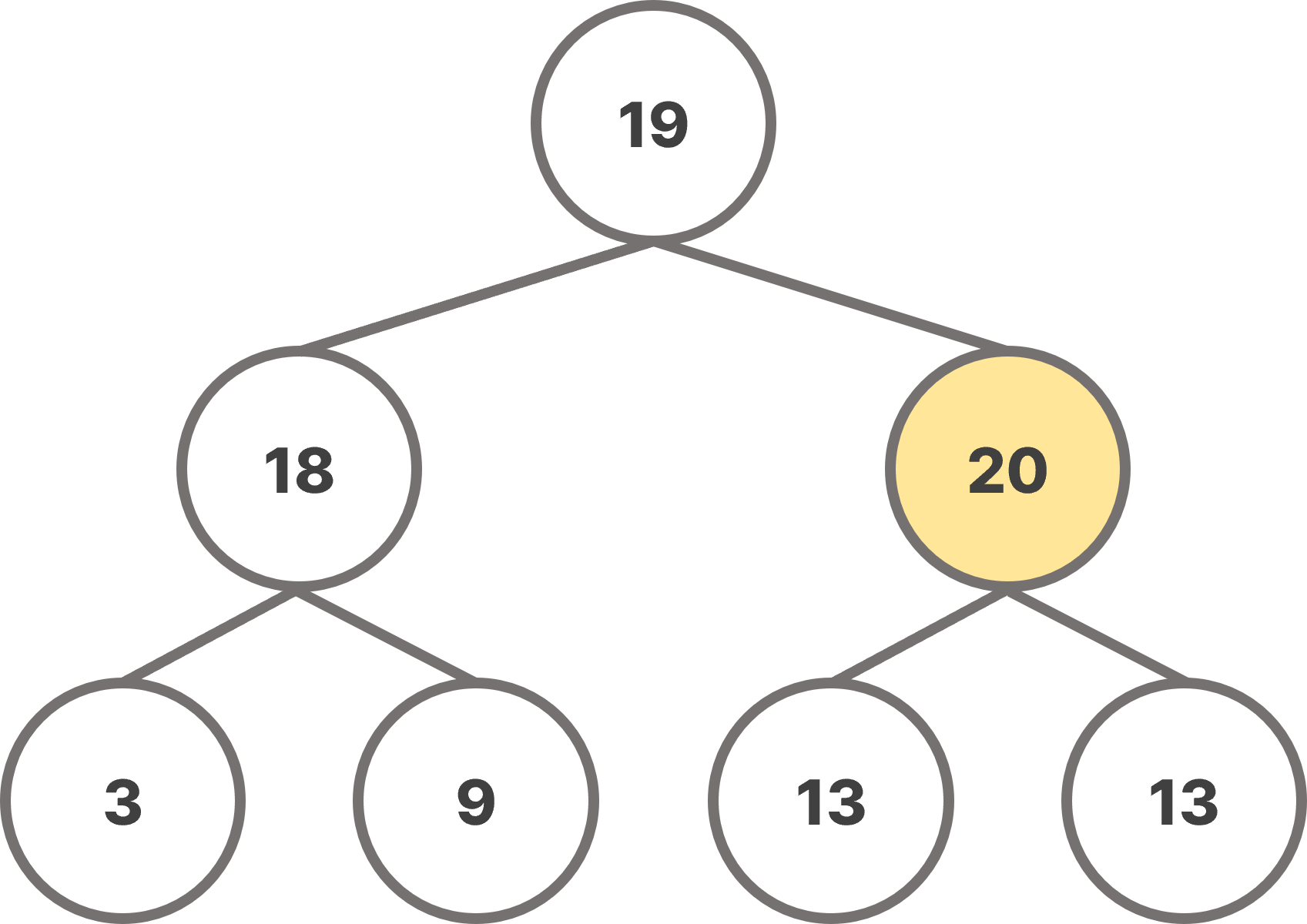
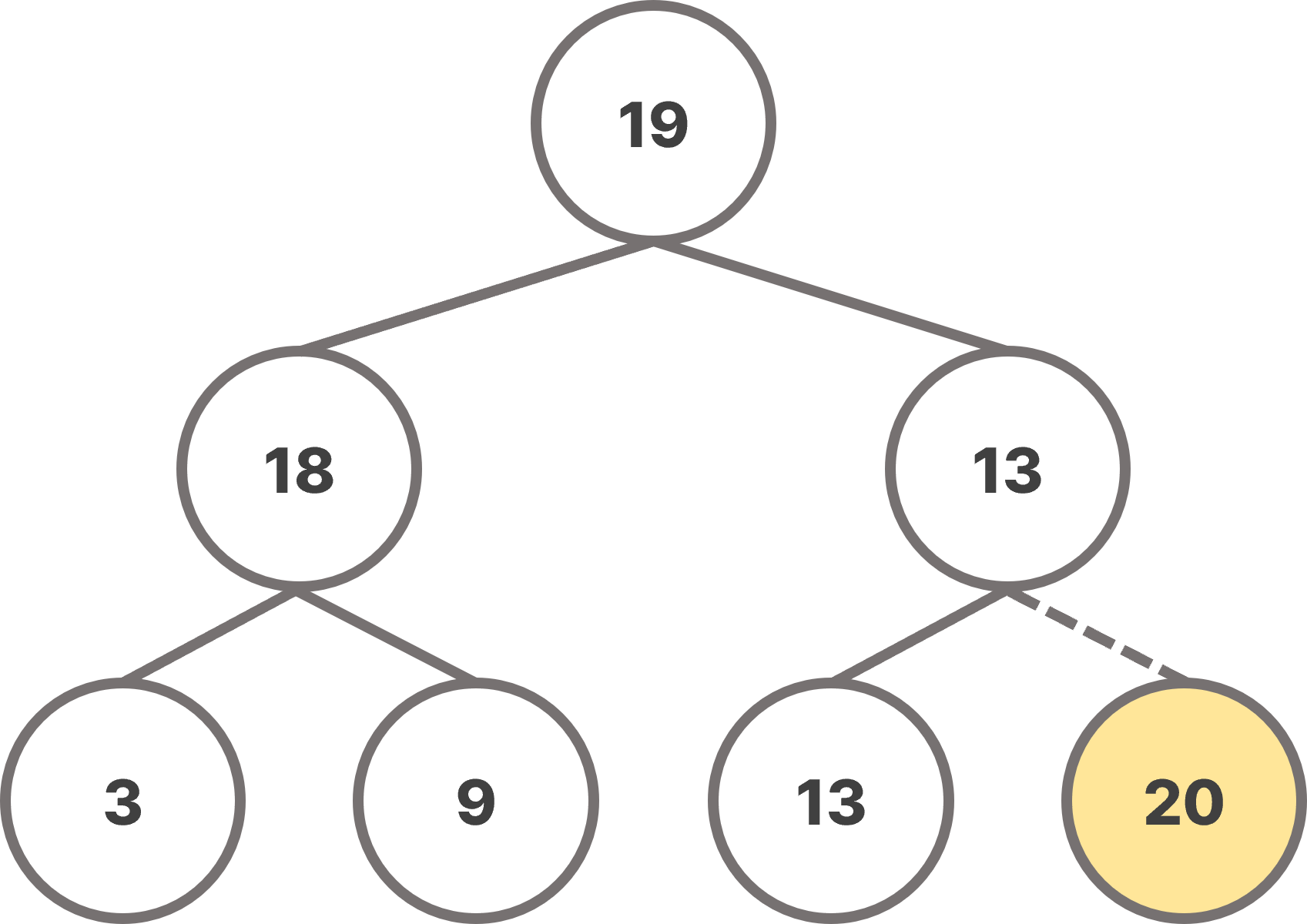
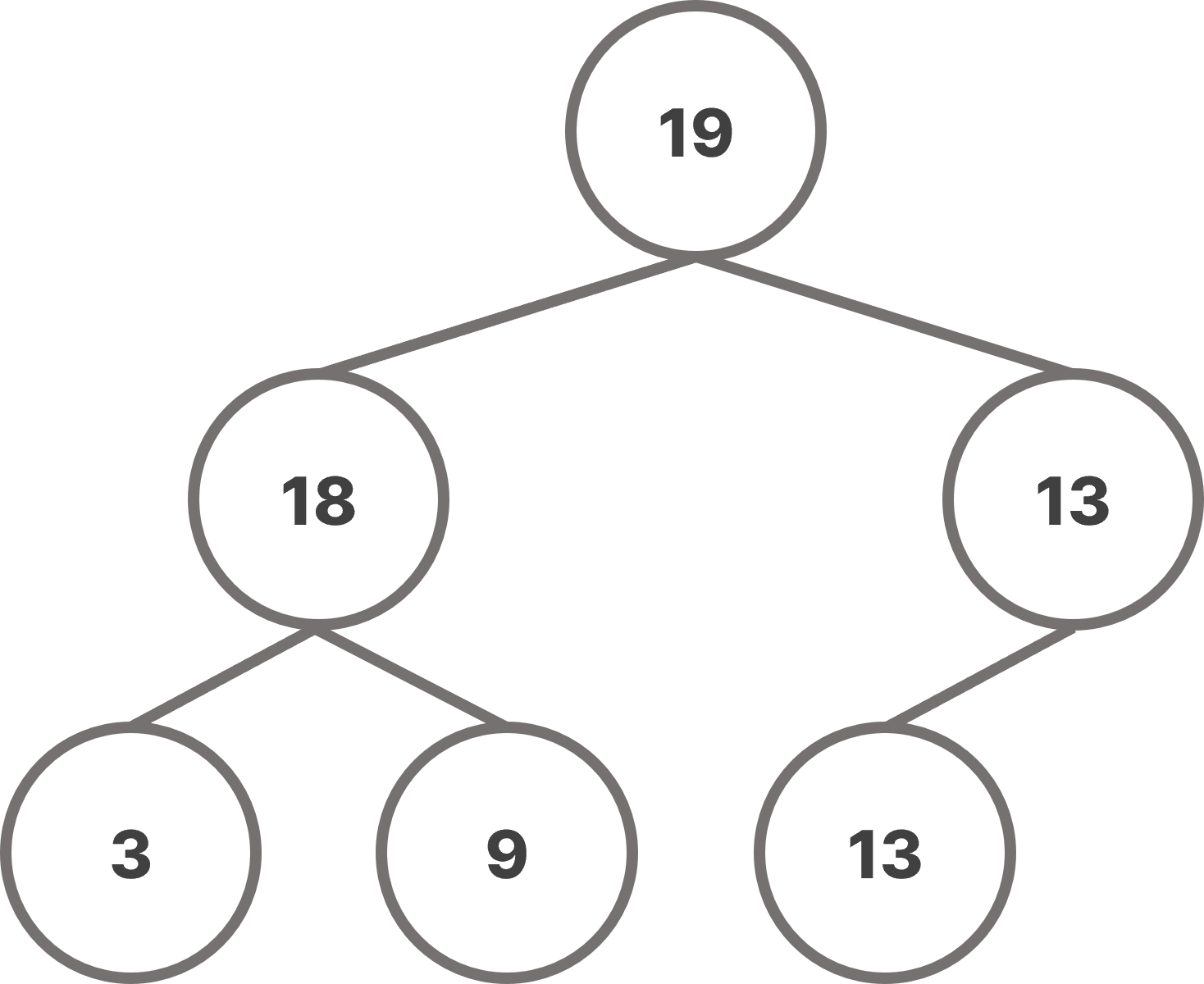
root 노드를 삭제할 때, 그냥 삭제하게 되면 heap의 구조가 붕괴되므로, 자식 노드 중 오른쪽 노드와 값을 교환해가며 heap 구조의 마지막 노드로 이동시킨 후 삭제한다.
수도코드는 다음과 같다.
void reheapDown (HEAP *heap, NODE *root, int last) {
if (root->left) {
int leftKey = root->left->key;
if (root->right) {
int rightKey = root->right->key;
}
else {
int rightKey = NULL;
}
}
if (leftKey > rightKey) {
largeSubtree = root->left;
}
else {
largeSubtree = root->right;
}
if (root->key < largeSubtree->key) {
swap(root, largeSubtree);
reheapDown(heap, largeSubtree, last);
}
}

